Explain refraction of light the basis of wave theory : Hence prove the laws of refraction.
Two coherent sources of light having intensity ratio $81 : 1$ produce interference frings Calculate the ratio of intensitites at the maxima and minima in the interference pattern.

Video Solution

Text Solution

Verified by Experts

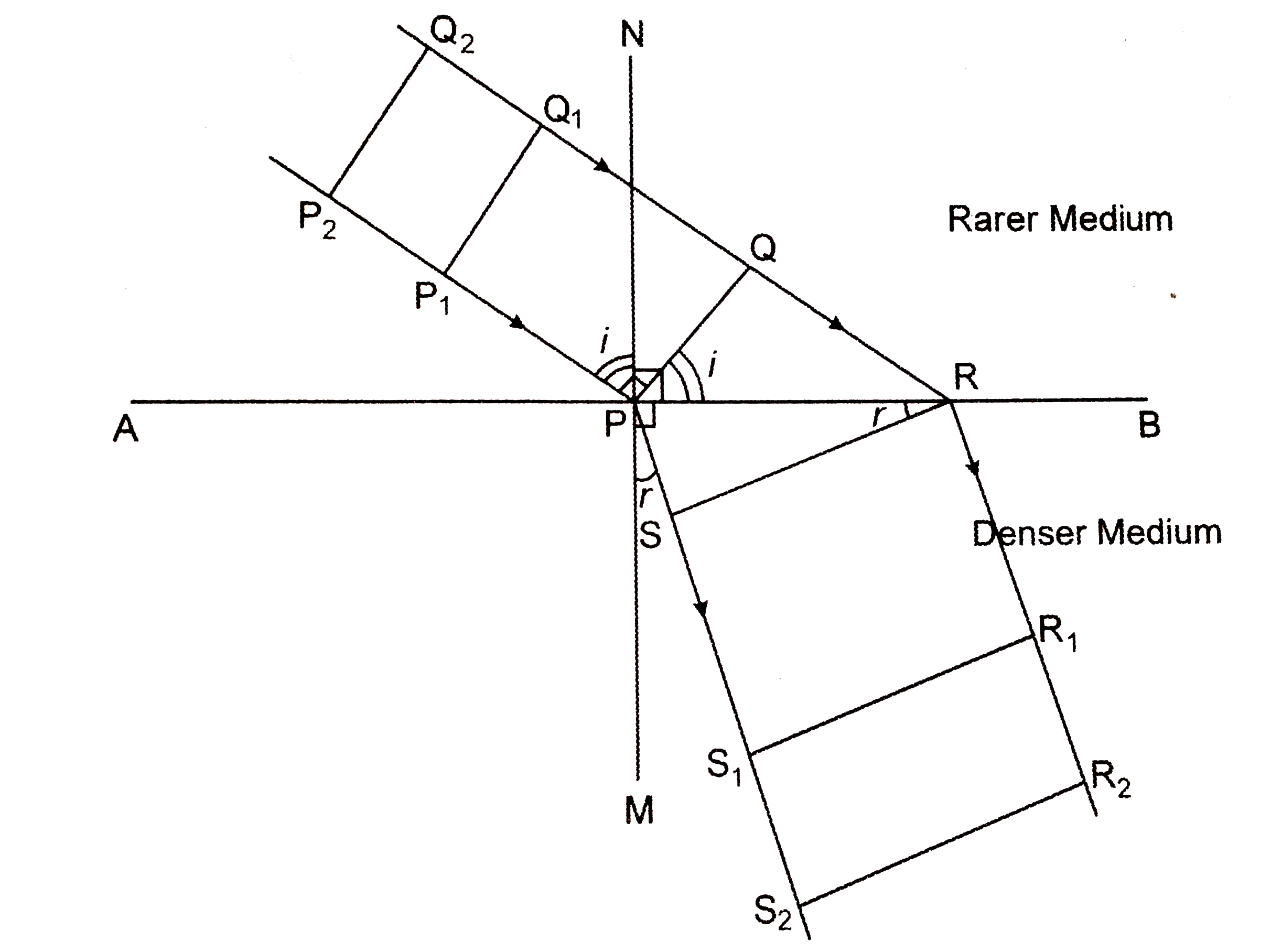
Consider a polane wavefront of monochromatic light obliquely incident at a plane refracting surface AB sperating two me mediums. Let $P_{2} Q_{2}, P_{1} Q_{1} and P Q$ be the successive positions of the incident wavefront. As soon as the wavefront reaches the point P, accroding to Huyge's principle's, it becomes th secondary source and emites secondary waves in the denser medium.
Let $v_{1} and v_{2}$ be the speed of light in rarer medium and the denser medium respectively. If t is the time taken by the incident ray to coer the distance QR, then Qr $v_{1} t$ . During this time the secondary wave originating from P will cover a distance $v_{2} t$ in the denser medium. Hence. the secondary spherical wavefront has a radiys $v_{2} t$ .
With P as centre, draw, a hemisphere or radius $v_{2} t$ in the denser mediy. Draw a tangent Rs to the secondary wavefron. RS represents a refracted wavefront.
$R_{1} S_{1} and R_{2} S_{2}$ are the successive positions of the refracted wavefronts . Draw NPM normal to AB at point P.
Now, $∠ P_{2} P N$ =i= angle of incidence
$∠ M P S_{2}$ =r= angle of refraction
From teh figure,
$∠ P_{2} P N + ∠ N P Q = 90^{\circ}$
$∠ N P Q + ∠ Q P R = 90^{\circ}$
$∴ ∠ P_{2} P N = ∠ Q P R = i$
Alos, $∠ M P S_{2} + ∠ S_{2} R P = 90^{\circ}$
$∠ S_{2} P R + ∠ P R S = 90^{\circ}$
$∴ M P S_{2} = ∠ P R S = r$
From $Δ P Q R = sin i = \frac{Q R}{P R}$
From $Δ R S P, sin d r = \frac{P S}{P R}$
$∴ \frac{sin i}{sin r} = \frac{Q R / P R}{P S / P R} = \frac{Q R}{P S}$
$\frac{sin i}{sin r} = \frac{v_{1} t}{v_{2} t}$
$∴ \frac{sin i}{sin r} = \frac{v_{i}}{v_{2}}$
But by definition,
$_{1} μ_{2} = \frac{Speed of light in medium1}{speed of light in medium 2}$
$_{1} μ_{2} = \frac{v_{1}}{v_{2}}$ = constant
$\frac{sin i}{sin r} =_{1} μ_{2}$
This is Snell's law of refraction.
Also, it can be seen from the figure that the incident ray and the normal and all three of them lie in the sample plane.
Thus, the laws of refractioin of light can be explained on the basis of Huyge's wave theory.

Numerical
Given $\frac{I_{1}}{I_{2}} = \frac{81}{1}$
$I \propto a^{2}$
$∴ \frac{I_{1}}{I_{2}} = \frac{a_{1}^{2}}{a_{2}^{2}} = \frac{81}{1}$
$\frac{a_{1}}{a_{2}} = \frac{9}{1}$
$\frac{I_{max}}{I_{min}} = \frac{{(a_{1} + a_{2})}_{1}^{2}}{{(a_{1} - a_{2})}_{1}^{2}}$
$\frac{I_{max}}{I_{min}} = \frac{{(9 + 1)}^{2}}{{(9 - 1)}^{2}}$
$\frac{I_{max}}{I_{min}} = \frac{100}{64} = \frac{25}{16}$
$\frac{I_{max}}{I_{min}} = \frac{25}{16}$

Updated on:21/07/2023

Two coherent sources of light of intensity ratio n are employed in an interference experiment. The ratio of the intensities of the maxima and minima in the interference pattern is
A $(\frac{n + 1}{n - 1})$
B ${(\frac{n + 1}{n - 1})}^{2}$
C $(\frac{\sqrt{n} + 1}{\sqrt{n} - 1})$
D ${(\frac{\sqrt{n} + 1}{\sqrt{n} - 1})}^{2}$
Two coherent sources of intensity ratio $1 : 4$ produce an interference pattern. The fringe visibility will be
A(a) $1$
B(b) $0.8$
C(c) $0.4$
D(d) $0.6$
If the amplitude ratio of two sources producing interference is 3 : 5, the ratio of intensities at maxima and minima is
A $25 : 16$
B $5 : 3$
C $16 : 1$
D $25 : 9$