State Brewster law and show that when light is incident at polarzing angle the reflected and refracted rays are mutually perpendicular to each other.
Mono chromatic light of wavelenght 4300 Å falls on slit of width 'a' For what value of a the first maximum falls at $30^{\circ}$ ?

Video Solution

Text Solution

Verified by Experts

Brewster's law : The tangent of polarising angle is eqaul to the refractive index of the medium with respect to th surrounding $(_{1} n_{2})$ at which partial reflection take place.
If $i_{p}$ is the polarsing angle,
Then ${tan i}_{p} =_{1} n_{2} = \frac{n_{2}}{n_{1}}$

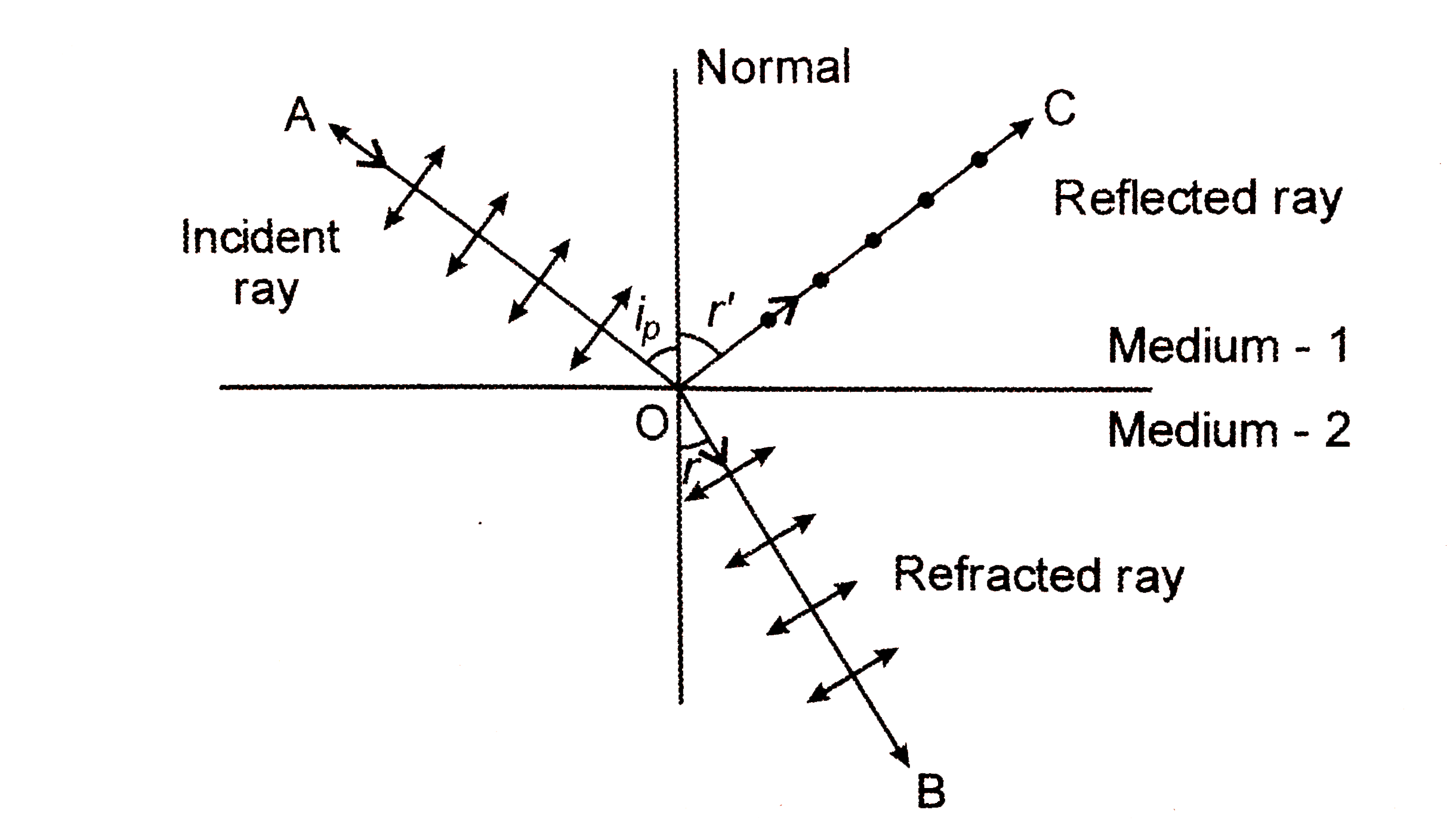
When $n_{1}$ is the absolute refractive index of the surrounding and $n_{2}$ is that the reflecting medium. In figure a ray of unpolarized light incident on the interface seperating two mediums. The degree of polarisation of the reflected ray OC varies with the angle of incidence and is maximum for the angle of incidence equal to the polarising angle $i_{p}$ for the paid of medium. For all angles of incidence, the refracted ray OB is only partially polarised.
Numerical :
Given :
$λ = 4300 Å = 4300 \times 10^{- 10} \times 10^{- 10} m$
$∴ a = \frac{3}{2} \cdot \frac{λ}{sin θ}$
$∴ a = \frac{3}{2} \cdot (4.3 \times) \frac{10^{- 7}}{{sin 30}^{\circ}}$
$a = 12.9 \times 10^{- 7} m$
or $a = 1.29 μ m$
By Snell's law, $μ = \frac{{sin i}_{p}}{sin r} ... (i)$
By Brewster's law
$μ = {tan i}_{p} ... (i i)$
From equation (i) and (ii)
$\frac{{sin i}_{p}}{sin r} = {tan i}_{p}$
$\Rightarrow \frac{{sin i}_{p}}{sin r} = \frac{{sin i}_{p}}{{cos i}_{p}}$
$∴ cos sin r = {cos i}_{p}$
or ${cos i}_{p} = sin r$
$\Rightarrow (sin (90 - i_{p}) = sin r$
$∴ 90 - i_{p} = r$
$\Rightarrow i_{p} + r = 90^{\circ}$
From the figure :
$i_{p} + ∠ B O C + r = 180^{\circ} (∴ i_{p} = r)$
$∴ ∠ B O C = 90^{\circ}$
$∴$ Angle between reflected and refracted ray is $90^{\circ}$

Updated on:21/07/2023