A thin nonconducting ring of radius R has a linear charge density λ = λ0 cos φ where λ0 is a constant φ is the azimuthal angle. Find the magnitude of the electric field strength a at the centre of the ring; b on the axis of the ring as a function of the distance x from its centre. Investigate the obtained function at x >> R.
a The given charge distribution is shown in Fig. The symmetry of this distribution implies that vector E at the point O is directed to the right and its magnitude is equal to the sum of the projection onto the direction of vectors E of vector dE from elementary charges dq. The projection of vector dE onto vector E isIt should be noted that this integral is evaluated in the most simple way if we take into account thatb Take an element S at an azimuthal angle φ from the x-axis the element subtending an angle dφ at the centre.The elementary field at P due to the element isThe component alon OS can be broken into the parts along OX and OY with
Related Solutions
A thin nonconducting ring of radius R has a linear charge density lambda = lambda_(0) cos varphi , where lambda_(0) is a constant , phi is the azimuthal angle. Find the magnitude of the electric field strength (a) at the centre of the ring , (b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x gt gt R .
View SolutionA thin non-conducting ring of radius R has a linear charge density lambda=lambda_(0)cosphi, where lambda_(0) constant and phi is the azimuthal angle. Find the magnitude of the electric field at the centre at the ring.
View SolutionA thin nonconducting ring of radius has a linear charge density , where is a constant , is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance from its centre. Investegation the obtained function at .
View SolutionA thin nonconducting ring of radius r has a linear charge density , where is a constant and is the angle at the centre from the diameter of maximum charge density in the anticlockwise direction. Find the electric field at the centre of the ring.
View SolutionThe linear charge density on a ring of radius R is where is a constant and is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
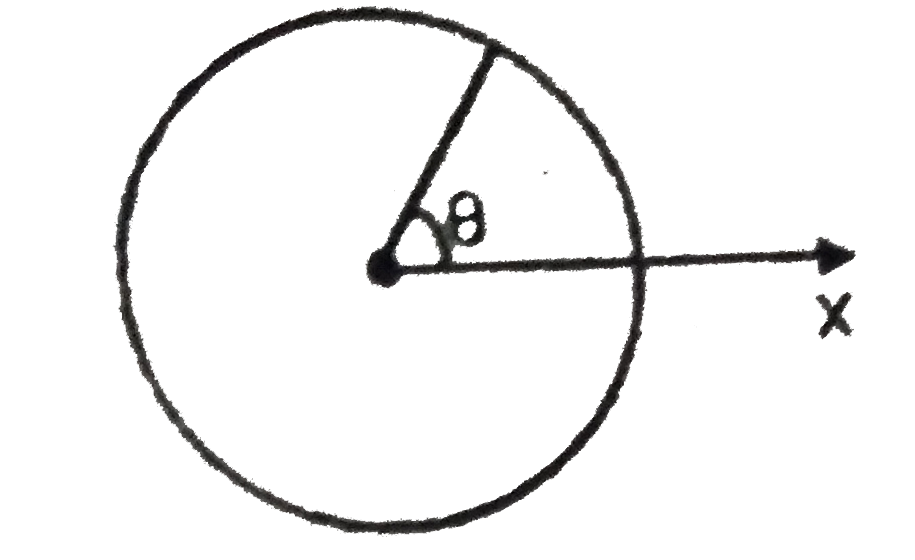
View SolutionThe linear charge density on a ring of radius R is lambda=lambda_0 sin (theta) where lambda_0 is a constant and theta is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
View SolutionA thin wire ring of radius "r" carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L gtgt r. Find maximum field strength and the corresponding distance L.
View SolutionA point charge is located at the centre fo a thin ring of radius with uniformly distributed charge , find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance from its centre, if .
View SolutionA point charge q is located at the centre of a thin ring of radius R with uniformly distributed charge "-q". Find the magnitude of the electric field strength vector at the point lying on the axis of the ring at a distance x from its centre if .
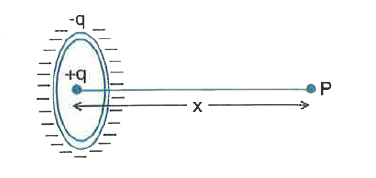
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge -q , find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x gt gt R .
View SolutionA charge is uniformly distributed over a quarter circular ring of radius . The magnitude of electric field strength at the centre of the ring will be
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
View SolutionConsider a uniformly charged ring of radius R and total charge Q. What is the magnitude of maximum possible electric field intensity on the axis of ring? What is the distance of point from the centre of ring at which the electric field is maximum?
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is lamda
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is lamda
View SolutionA thin circular ring of radius r is charged uniformaly so that its linear charge density becomes . Derive an expression for the electric for the electric field at a point P at a distance x from it along the axis of the ring. Hence, prove that at large distances (x>>r), the ring behaves as a point charge.
View SolutionA quarter ring of radius R is having uniform charge density lambda . Find the electric field and potential at the centre of the ring.
View Solution