A thin non-conducting ring of radius R has a linear charge density where constant and is the azimuthal angle. Find the magnitude of the electric field at the centre at the ring.
Radius of the non-conducting ring = R
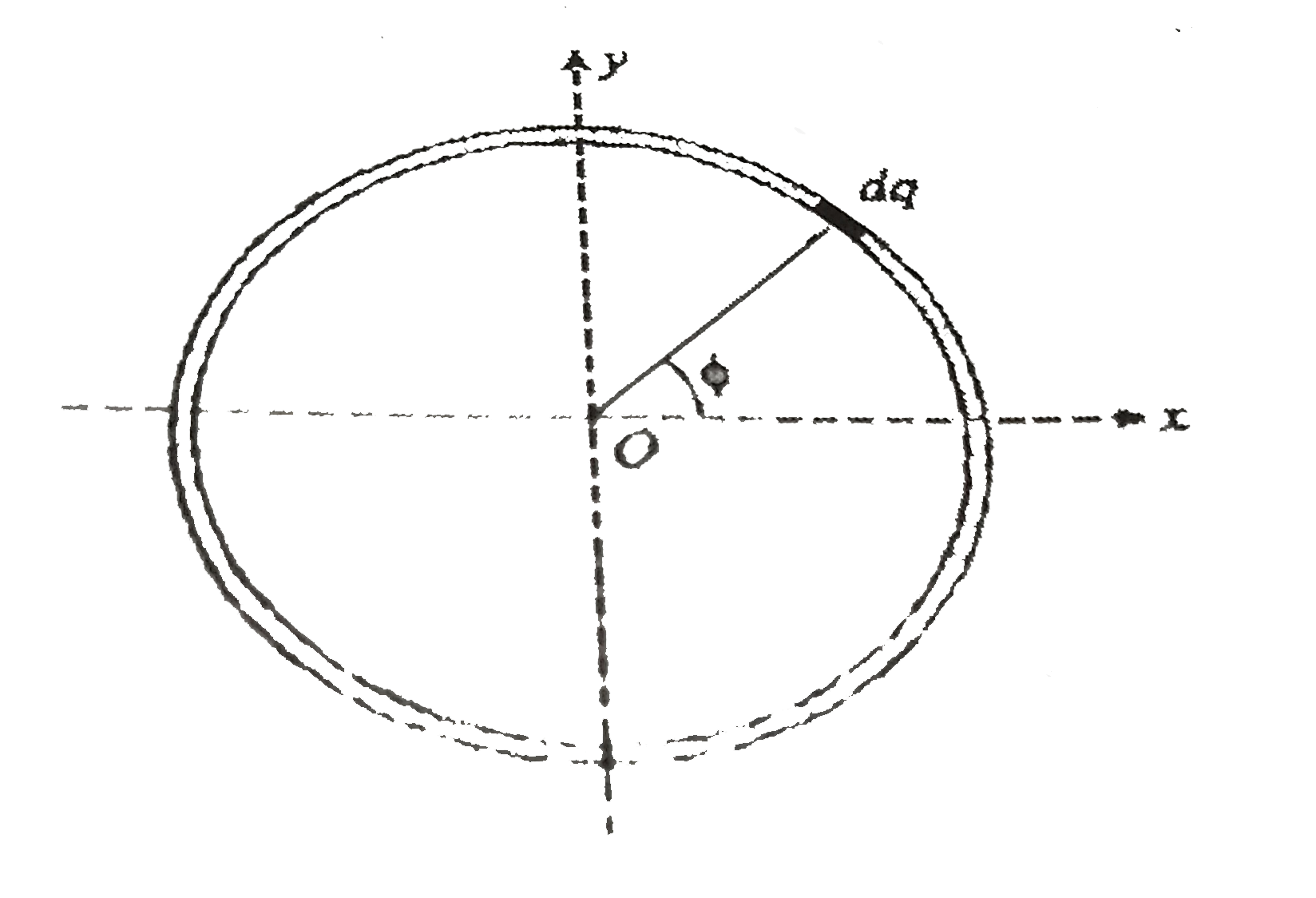
Linear charge density where is azimuthal angle. The variation of chare along the ring is shown in fig (2).
Consider a small segment of ring making an angle at the centre. Charge on this segment . Electric field due to this element charge at centre is dE.
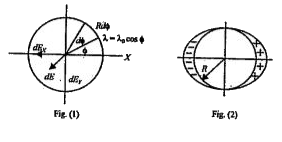
dE contains two components .
Then
or
Therefore E at the curve is equal to directed along the x-axis.
Similar Questions
A thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View Solution
Knowledge Check
A thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is
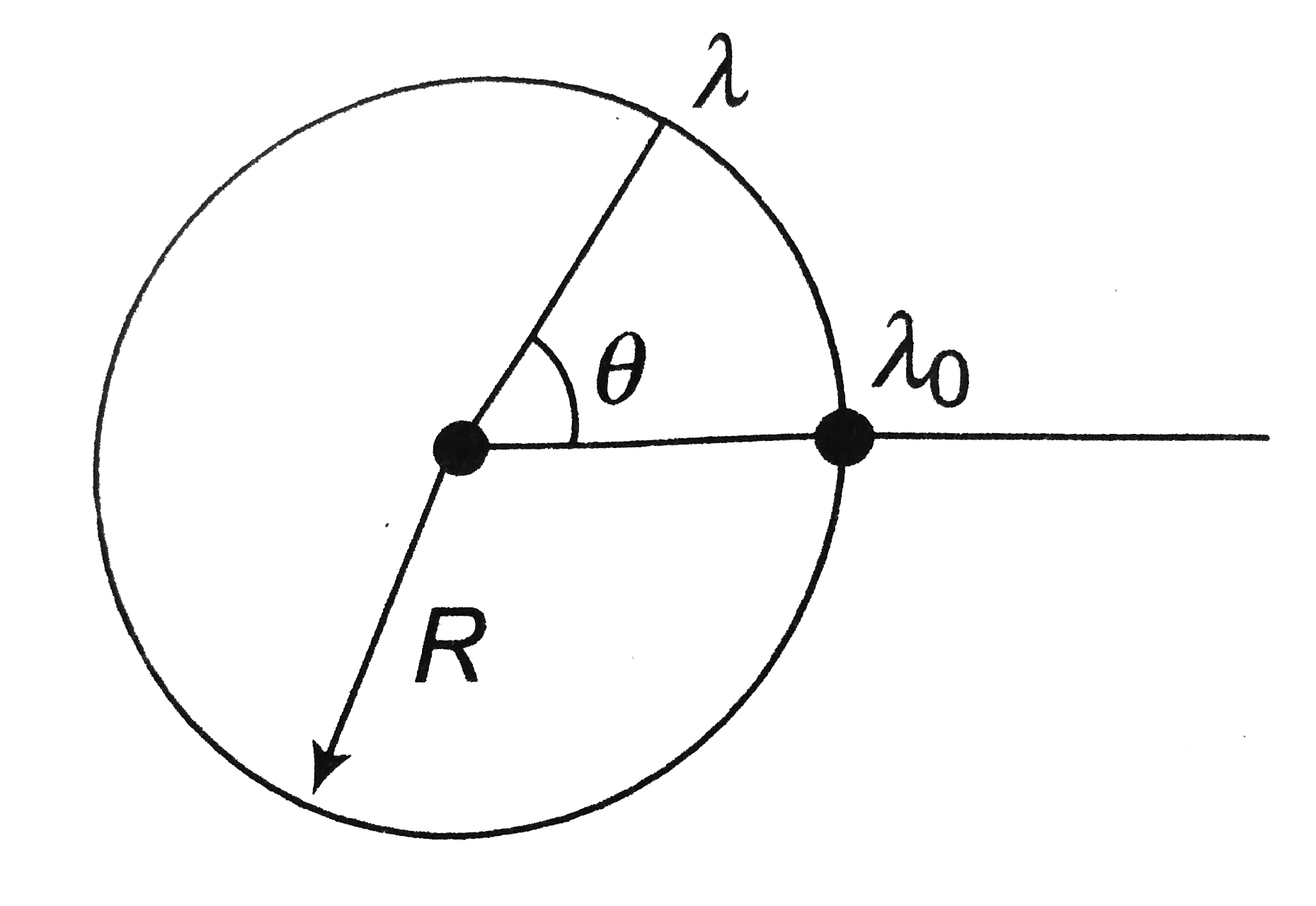 AR2λ0B2πR2λ0CπR2λ02DπR2λ0
AR2λ0B2πR2λ0CπR2λ02DπR2λ0A non conducting ring of radius R1 is charged such that the linear charge density is λ1cos2θ where θ is the polar angle. If the radius is increased to R2 keeping the charge constant, the linear charge density is changed to λ2cos2θ. The relation connecting R1, R2λ1 and λ2 will be
Aλ1/R1=λ2/R2Bλ1/R2=λ2/R1Cλ1λ2=R1R2Dλ21R1=λ22R2The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
 A0Bλ0∈0Cλ0π∈0Dλ02π∈0
A0Bλ0∈0Cλ0π∈0Dλ02π∈0
A thin nonconducting ring of radius r has a linear charge density q=q0cosθ, where q0 is a constant and θ is the angle at the centre from the diameter of maximum charge density in the anticlockwise direction. Find the electric field at the centre of the ring.
View SolutionA thin non-conducting ring or radius a has a linear charge density λ=λ0sinϕ. A uniform electric field E0ˆi+E0ˆj exist in the region . .Net torque acting on ring is given as :
View SolutionA thin non-conducting ring or radius a has a linear charge density λ=λ0sinϕ. A uniform electric field E0ˆi+E0ˆj exist in the region . .Net torque acting on ring is given as :

View SolutionA non conducting ring of radius R1 is charged such that the linear charge density is λ1cos2θ where θ is the polar angle. If the radius is increased to R2 keeping the charge constant, the linear charge density is changed to λ2cos2θ. The relation connecting R1, R2λ1 and λ2 will be
View SolutionThe linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is

View Solution

