A cubical block of iron 5cm on each side is floating on mercury in a vessel:- 1 What is the height of the block above mercury level? 2 Water is poured into vessel so that it just covers the iron block. What is the height of the water column? Given Density of mercury = 13.6g|cm3 and Density of iron = 7.2g|cm3
1 Let h = height of cubical block above mercury level Volume of cubical Iron Block = l × b × h = 5 × 5 × 5 = 125 cm3.Mass of cubical Iron Block = Volume × Density of Iron= 125 × 7.2= 900 g → 1 Volume of Mercury displaced = Length × Breadth × Decreased height = l × b × 5 – h = 5 × 5 × 5 – h Mass of Mercury displaced = Volume of Mercury × Density of Mercury = 5 × 5 × 5 – h × 13.6 → 2 2 When water is poured let x = height of block in water∴Depth of block in mercury = 5 – x cmMass of water displaced = 5 × 5 × x × 1 = 25 x gm 1 = Density of water in g|cm3 Mass of Mercury displaced = 5 × 5 × 5 – x × 13.6 = 25 X 13.6 5 – x gm Acc. to principle of floatation Weight of Iron Block = Weight of water displaced + Weight of mercury displaced
Related Solutions
A cubical block of iron, 5 cm on each side is floating in mercury taken in a vessel. What is the height of the block above mercury level.
View SolutionEach side of an iron cube is 5 cm. This cube floats on mercury. What height of the cube remains above the surface of mercury? To cover the cube, if water is poured over mercury, then what will be the height of the water column? The density of iron is and the density of mercury is .
View SolutionA cubical block of iron of side 5 cm is floating in mercury taken in a vessel. What is the height of the block above mercuery level. (rho_(Hg)=13.6g//cm^(3),rho_(Fe)=7.2g//cm^(3))
View SolutionA cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ? (ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6 gm//cm^(3) . Density of iron 7.2 gm//cm^(3)
View SolutionA vessel contains mercury and water. An iron cylinder just floats vertically in that vessel. What is the ratio of the immersed parts of the cylinder in water and in mercury? The density of mercury = and the density of iron = .
View SolutionA cubical block of iron of side 13.6 cm is floating in mercury in a vessel .Water is poured in the vessel until it just covers the iron block. What is the height of water column? ( rho_Hg=13.6gm/cm^3 , rho_Fe=7.2 gm/cm^3 , rho_H_2O=1 gm/cm^3 )
View SolutionA cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are . The height of the block above the mercury level is given by
View SolutionA cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are rho_(s) " and " rho_(m) . The height of the block above the mercury level is given by
View Solutionस्टील से निर्मित किसी घन के ब्लॉक की भुजा e है जो पारे से से भरे पात्र में पारे की सतह पर तैर रहा है यदि स्टील तथा पारे के घनत्व क्रमशः तथा है तो पारे की सतह से ऊपर ब्लॉक की ऊँचाई होगी
View SolutionA block of iron floats on mercury. Find the fractionof volume which remains immersed in mercury. (Densities of iron and mercury are and respectively).
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA cubical block of copper of side 10 cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
View SolutionA cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is ( rho_(Hg) = 13.6 g//c c , rho_(Cu) = 7.3 g//c c , rho_(water) = 1gm//c c)
View SolutionThe density of ironis 7.8 g/c.c and that of mercury is 13.6 g/c.c. Therefore, an iron block will float on mercury.
View SolutionA cylinder of iron floats vertically and fully immersed in a vessel containing mercury and water. Find the ratio of the length of the cylinder immersed in water to that immersed in mercury. (Relative density of mercury = 13.6 and that of iron = 7.78)
View SolutionTwo vessels connected to each other are filled with mercury. The diameter of one vessel is n times greater than the diameter of the other vessel. If a column of height h of water is poured into the left vessel, then by how much will the level of mercury rise in the right hand vessel? (s = relative density of mercury and rho = density of water)
View SolutionMercury of density is poured into cylinderical communicating vessels of cross-sectional area 2A and A respectively. A solid iron cube of volume and relative density 2 is dropped into the broad vessel, and as a result the level of the mercury in it rises. Then, water is poured into the broader vessel until the mercury reaches the previous level in it. Find the height of water column if it does not submerge the block.
View SolutionMercury of density rho_(m) is poured into cylinderical communicating vessels of cross-sectional area 2A and A respectively. A solid iron cube of volume V_(0) and relative density 2 is dropped into the broad vessel, and as a result the level of the mercury in it rises. Then, water is poured into the broader vessel until the mercury reaches the previous level in it. Find the height of water column if it does not submerge the block.
View SolutionTwo communicating vessels contain mercury. The diameter of one vessel is n times larger than the diameter of the other. A column of water of height h is poured into the left vessel (s=relate density of mercury and ) by
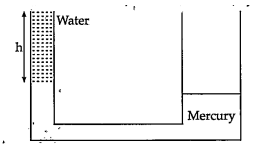
View Solution(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?
View Solution