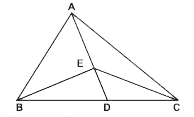
In figure E is any point on median AD of a ∆ABC. Show that arABE = arACE.
Construction: From A draw AG ⊥ BC and from E draw EF ⊥ BC. Proof : ar∆ABD = BD×AG/2 ar∆ADC = DC × G/2 But BD = DC [∴D is the mid-point of BC AD being the median] ar∆ABD = ar∆ADC ...i Again ar∆EBD= BD× EF/2 ar∆EDC = DC × EF/2 But BD = DC ∴ ar∆EBD = ar∆EDC ...ii Subtracting ii from i we get ar∆ABD - ar∆EBD = ar∆ADC - ar∆EDC ⇒ ar∆ABE = ar∆ACE.
Related Solutions
In the given figure, Delta ABC E is any point on the median of AD. show that ar (Delta ABE) = ar (DeltaACE)
View SolutionIn the given figure, Delta ABC E is any point on the median of AD. show that ar (Delta BED) = ar (DeltaCDE)
View SolutionIn the figure 11.23, E is any point on median AD of a ABC. Show that ar (ABE) = ar (ACE).
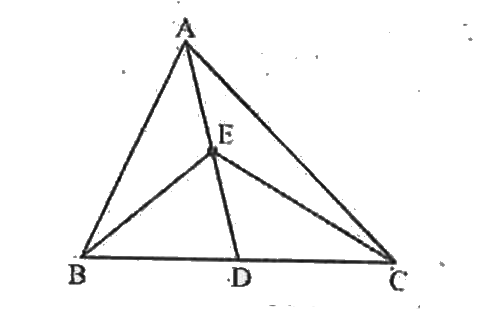
View SolutionIn the Given figure, E is any point on median AD of a Show that ar (ABE) = ar (ACE)
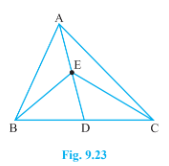
View SolutionIn Fig.9.23, E is any point on median AD of a . Show that
View SolutionE is any point on median AD of a . Show that ar (ABE) = ar (ACE).
View SolutionIn the adjoining figure,E is a point on the median AD of a Delta ABC. Show that ar (Delta ABE)=(Delta ACE)
View Solutionआकृति में, की एक मध्यिका AD पर स्थित E कोई बिंदु है दर्शाइए कि है।
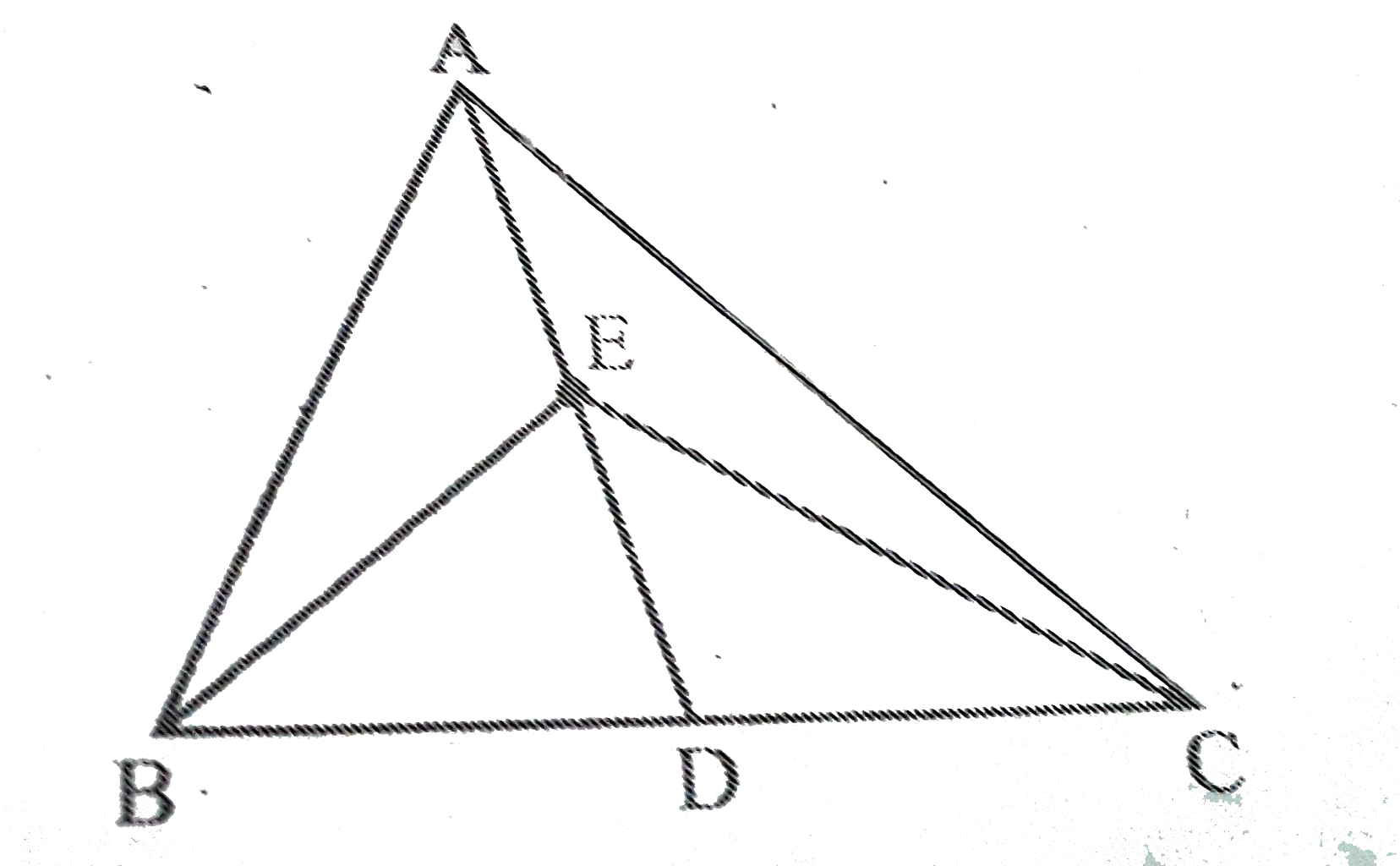
View SolutionIn the given figure, AD is median of and E is any point on median AD. Prove that Area = Area
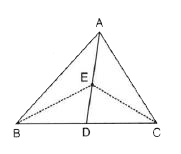
View SolutionIn the figure, E is any point on median AD of a triangleABC . Show that ar( triangleABE )= ar( triangleACE ).
View SolutionAD is the median of ABC and E is any point on AD. Which of the following statement is true ?
View Solutionis one of the medians of a is any point on . Show that
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = ar (ABC).
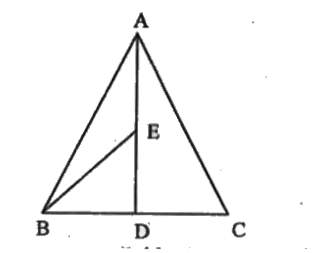
View SolutionIn a triangle ABC, E is the mid - point of median AD. Show that ar (BED) =1/4 ar (ABC)
View SolutionE is any point on median AD of a . Show that ar (ABE) = ar (ACE).
View SolutionIn a is the mid-point of median Show that
View SolutionIn A ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3:1.
View Solutionਚਿੱਤਰ 9.23 ਵਿੱਚ, ਦੀ ਇੱਕ ਮੱਧਿਕਾ AD ਉੱਤੇ ਸਥਿਤ E ਕੋਈ ਬਿੰਦੂ ਹੈ। ਦਰਸਾਉ ਕਿ ar (ABE) = ar (ACE) ਹੈ।
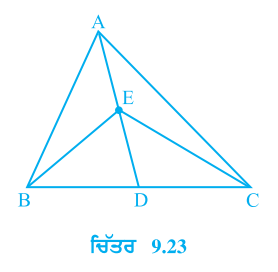
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (triangleBED)=1/4 ar( triangleABC ).
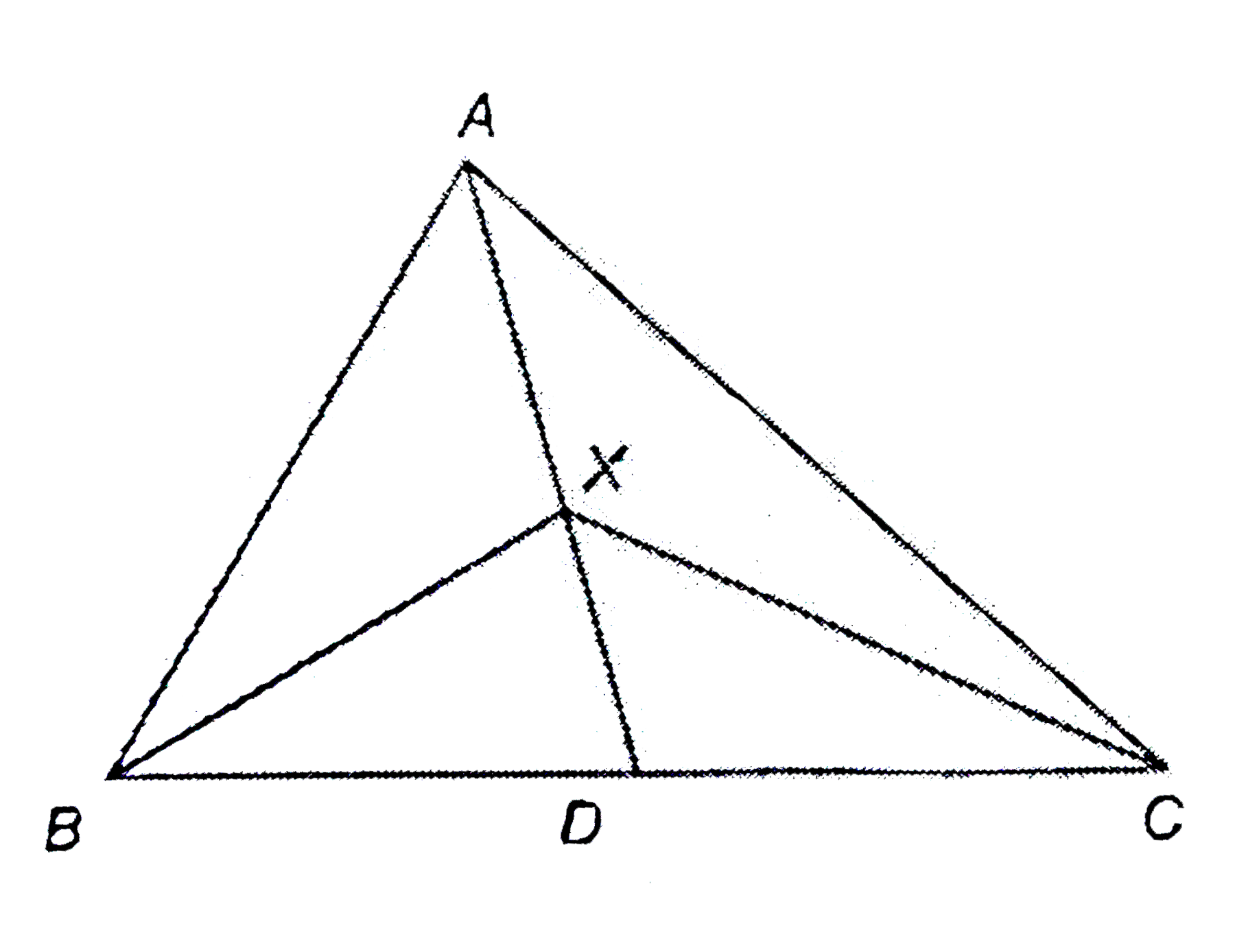
View SolutionIn the adjoining figure, AD is the median of and X be any point on side AD. Prove that:
area
View Solution