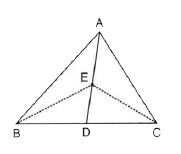
In the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

In ΔABC,
D is the mid-point of BC.
∴ area (ΔABD)= area (ΔACD)
(median divides the triangle into equal area) ..(1)
Again, in ΔXBC
D is the mid-point of BC
area (ΔXBD)= area (ΔXCD)
(.: median divides the triangle into two equal areas) ..(2)
Subtract (2) from (1), we get
area (ΔABD)− area (ΔXBD)= area (ΔACD)− area (ΔXCD)
⇒ area (ΔABX)= area (ΔACX)
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Problems From NCERT/exemplar
Explore 12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Exercise
Explore 34 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
Similar Questions
Knowledge Check
In the figure, what is the area of ΔABC?
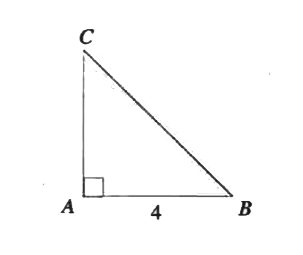 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenIn the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2
In the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
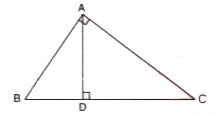
Prove that : ΔABD is similar to ΔCAD.
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC

View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View Solution