The medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
Let D is the mid-point of BC.
In ΔABC
D is the mid-point of BC
∴ area of ΔABD= area of ΔADC
(.: Median divides the triangle into two equal area)..(1)
In ΔGBC
D is the mid-point of BC
∴ area of ΔGBD= area of ΔGCD
(.: median divides the triangle into two equal area)..(2)
Subtract (2) from (1), we get
area of ΔABD− area of ΔGBD= area of ΔACD− area of ΔGCD
⇒ area of ΔABG= area of ΔACG....(3)
Similarly, we can prove that
area of ΔACG= area of ΔBCG
(∴ median divides the triangle into two equal area)...(4)
From (3) and (4), we get
area of ΔABG= area of ΔACG= area of ΔBCG
∴ area of ΔABG=13× area of ΔABC

Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Problems From NCERT/exemplar
Explore 12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Exercise
Explore 34 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
Similar Questions
In the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

View SolutionThe median BE and CF of a triangle ABC intersect at G. Prove that the area of ΔGBC= area of the quadrilateral AFGE.
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔOBD)= area (ΔOCE)
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔACD)= area (ΔABE)
View SolutionThe medians BE and CF of a triangle ABC intersect at G . Prove that area of △GBC=area of quadrilateral AGFE.
View SolutionThe base BC of triangle ABC is divided at D so that BD = 12 DC.
Prove that area of ΔABD=13 of the area of ΔABC.
View SolutionIn the following figure G, is centroid of the triangles ABC.
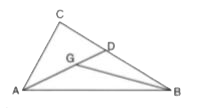
Prove that
Area (Δ AGB )=13× Area (ΔABC)
View SolutionIn triangle ABC, D is a point in side BC such that 2BD=3DC. Prove that the area of triangle ABD = 35×Area ofΔABC
View Solution

