The collar A slides on the smooth vertical bar. The masses mA = 20 kg and mB = 10 kg. When h = 0.1 m the spring is unstretched. When the system is in equilibrium h = 0.3 m. Determine the spring constant k.
The triangles formed by the rope segments and the horizontal line level with A can be used to determine the lengths Lu and Ls. The equations areThe stretch in the spring when in equilibrium is given by δ = Ls - Lu. Carrying out the calculations we get Lu = 0.269 m Ls = 0.391 m and δ = 0.121 m. The angle θ between the rope at A and the horizontal when the system is in equilibrium is given by tanθ =0.3/0.25 or θ = 50.2°. From the free body diagram for mass A we get two equilibrium equations. They are We have two equations in two unknowns and can solve. We get NA =163.5 N and T = 225.4 N Now we go to the free body diagram for B where the equation of equilibrium is T - mBg - kδ = 0. This equation has only one unknown. Solving we get k = 1297 N/m
Related Solutions
A collar of mass is at rest and when it is in the position shown, the spring is unstretched. If another collar of mass strikes it so that slides a distance on the smooth rod before momentarily stopping, determine the velocity of just after the impact. The coefficient of restitution is . The spring constant is .
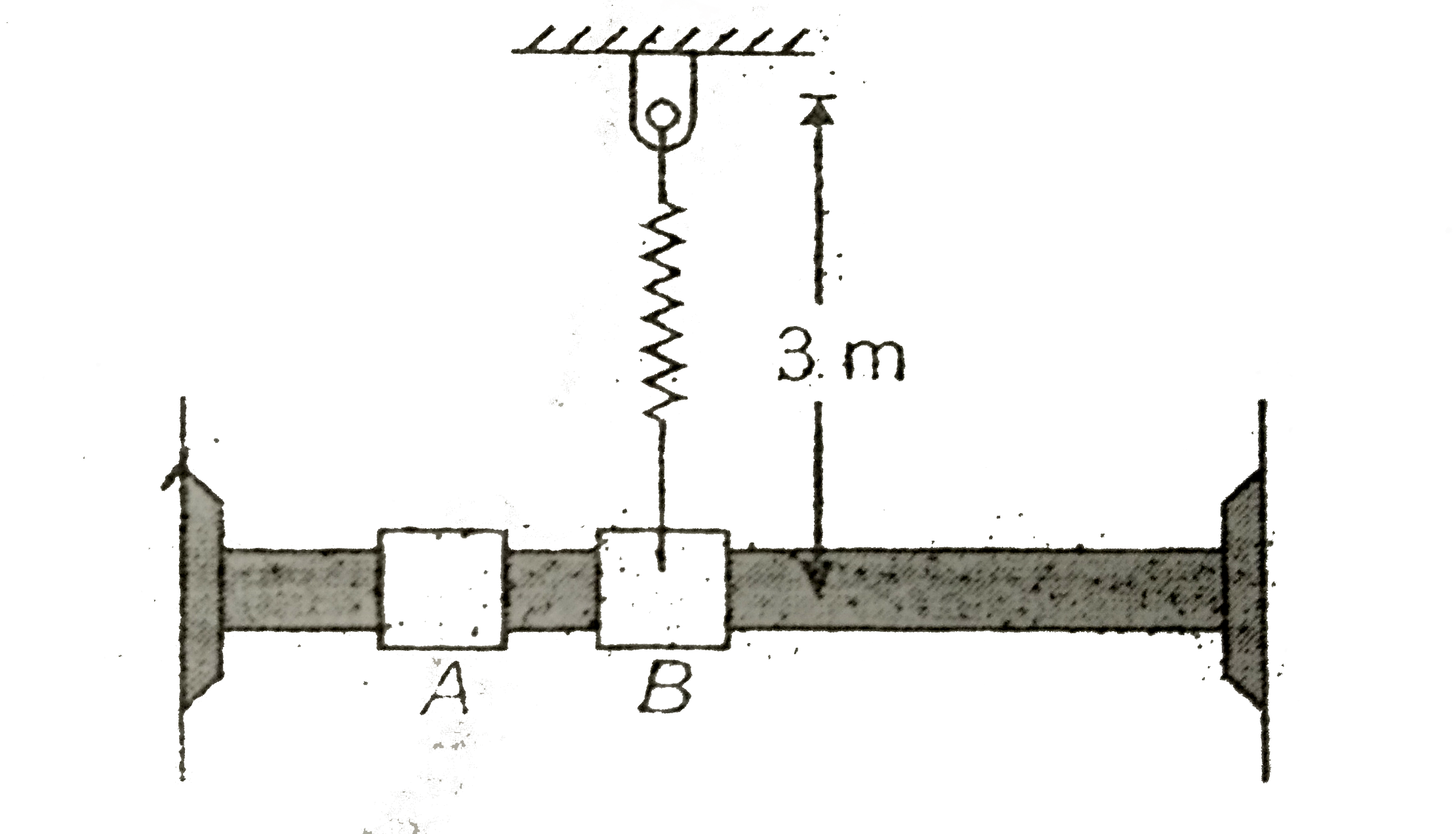
View SolutionA 10 kg collar is attached to a spring (spring constant 600 N/m.), it slides without friction over a horizontal rod. The collar iis displaced from the equilibrium position by 20 cm and released. What is the speed of the oscillation ?
View SolutionThree masses 0.1 kg, 0.3 and 0.4 kg are suspended at the end of the spring. When the 0.4 kg is removed, the system oscillates with a period of .2. sec. When 0.3 kg mass is also removed, the system will oscillate with a period
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is .
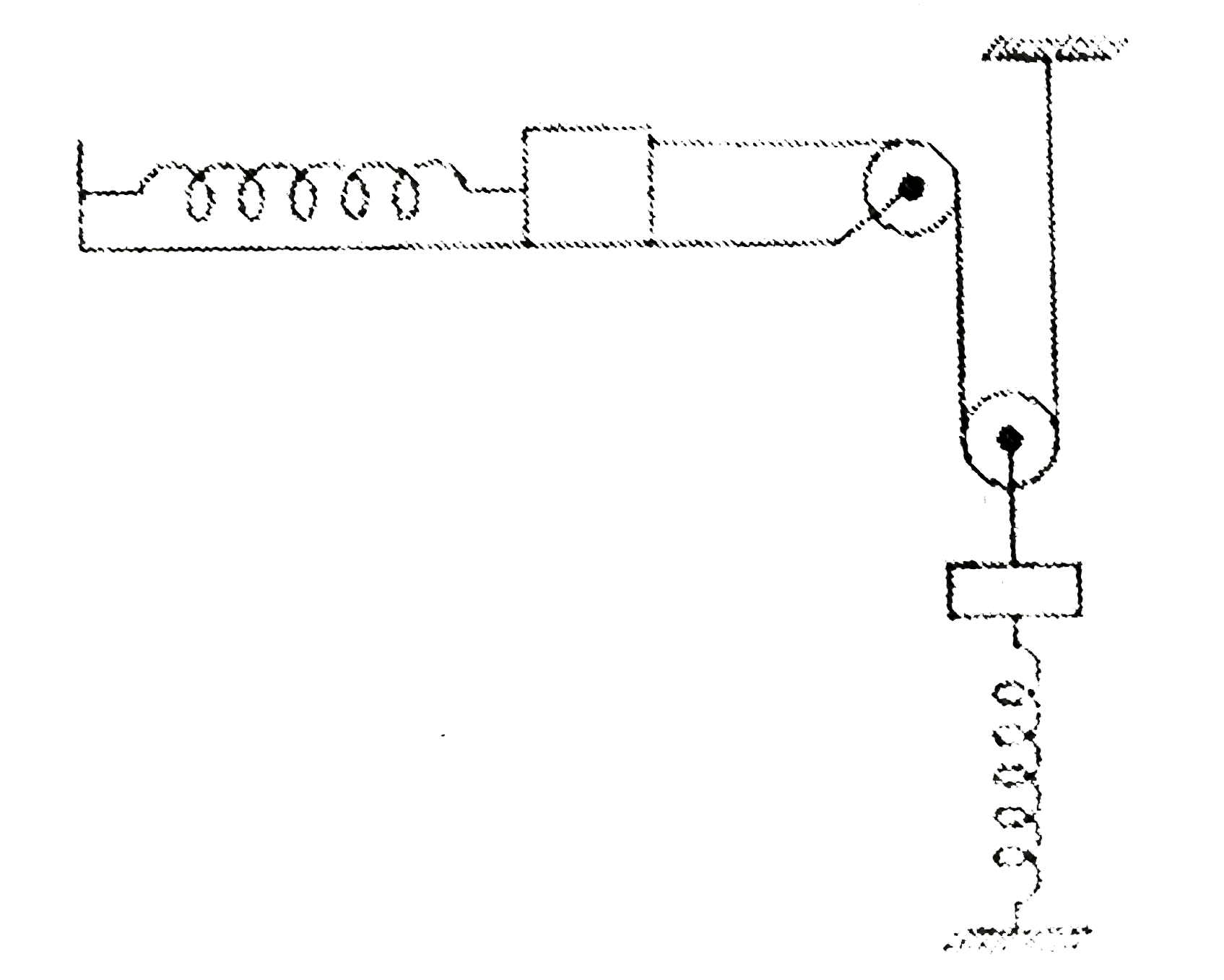
Extension of horizontal spring in equilibrium is
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m. Extension of horizontal spring in equilibrium is:

View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is .

Extension of horizontal spring in equilibrium is
View SolutionA spring when compressed by 0.2 m develops a restoring force of 50 N. If a body of mass 10 kg is placed on it, calculate
the force constant (K) of the spring
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . In the equilibrium position, speed of the block placed horizontally is
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . In the equilibrium position, speed of the block placed horizontally is
View SolutionA block of mass is connected to another block of mass by a massless spring of spring constant . the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force starts acting on the block of mass of pull it. Find the maximum extension of the spring
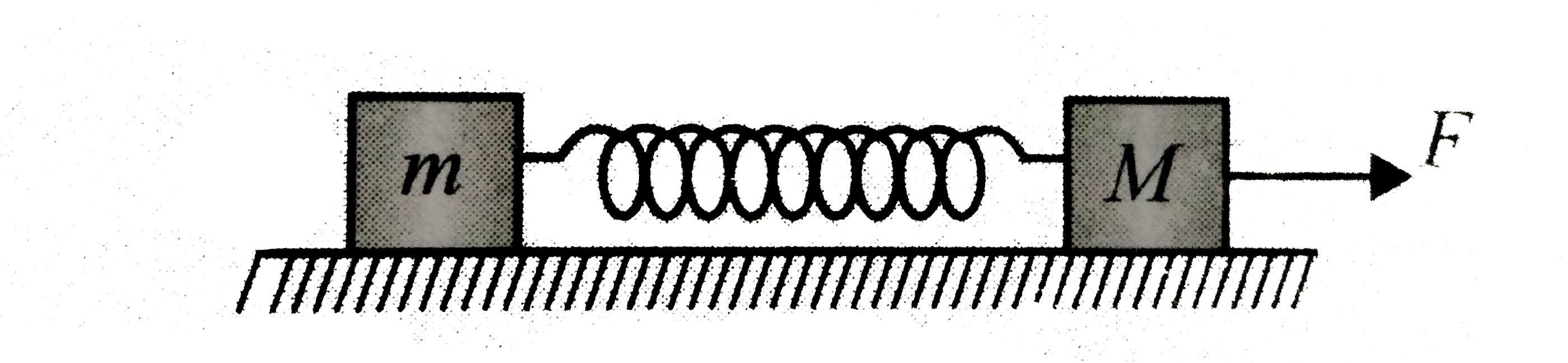
View SolutionA block of mass is connected to another block of mass by a massless spring of spring constant . the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force starts acting on the block of mass of pull it. Find the maximum extension of the spring
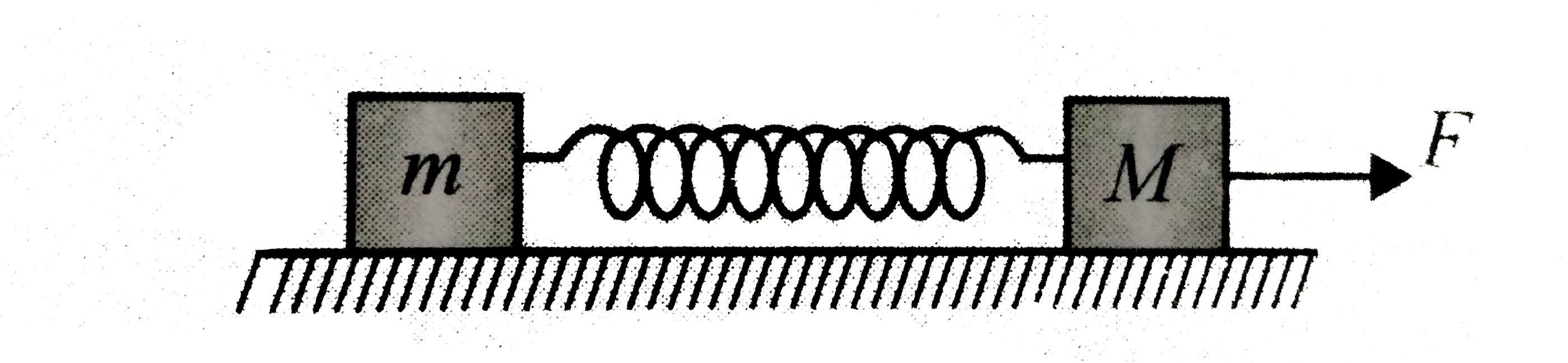
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially, the blocks are at rest and the spring is unstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solutionएक ऊर्ध्वाधर स्प्रिंग के निचले सिरे पर M द्रव्यमान का एक पिण्ड बंधा है। स्प्रिंग एक छत से लटका है तथा उसके बल नियतांक का मान k है। जब पिंड को मुक्त छोड़ा गया तो यह विराम अवस्था में था और स्प्रिंग बिना खिंचाव था। स्प्रिंग की लम्बाई में अधिकतम वृद्धि होगी:-
View SolutionA block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g = 10 ms^-2)
View Solutionએક 0.1 kg દળનો પદાર્થ ના વેગથી ગતિ કરી બળ અચળાંક ધરાવતી સ્પ્રિંગ સાથે અથડાઈ સ્થિર થઈ જાય છે, તો સ્પ્રિંગ કેટલી દબાશે ?
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)
View Solutionद्रव्यमान 0.1 किग्रा का एक पिण्ड वेग 10 मीटर/सेकण्ड से बल नियतांक 1000 न्यूटन/मीटर वाली एक स्प्रिंग से टकराता हैं ( स्प्रिंग का दूसरा सिरा कसा हैं ) तथा स्प्रिंग को सम्पीड़ित करने के पश्चात विराम पर आ जाता हैं | स्प्रिंग का सम्पीडन होगा :
View SolutionThree mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring. When is 0.4 kg mass is removed , the system oscillates with a period 2 s . When the 0.3 kg mass is also removed , the system will oscillates with a period
View SolutionThree mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring. When is 0.4 kg mass is removed , the system oscillates with a period 2 s . When the 0.3 kg mass is also removed , the system will oscillates with a period
View Solution