The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
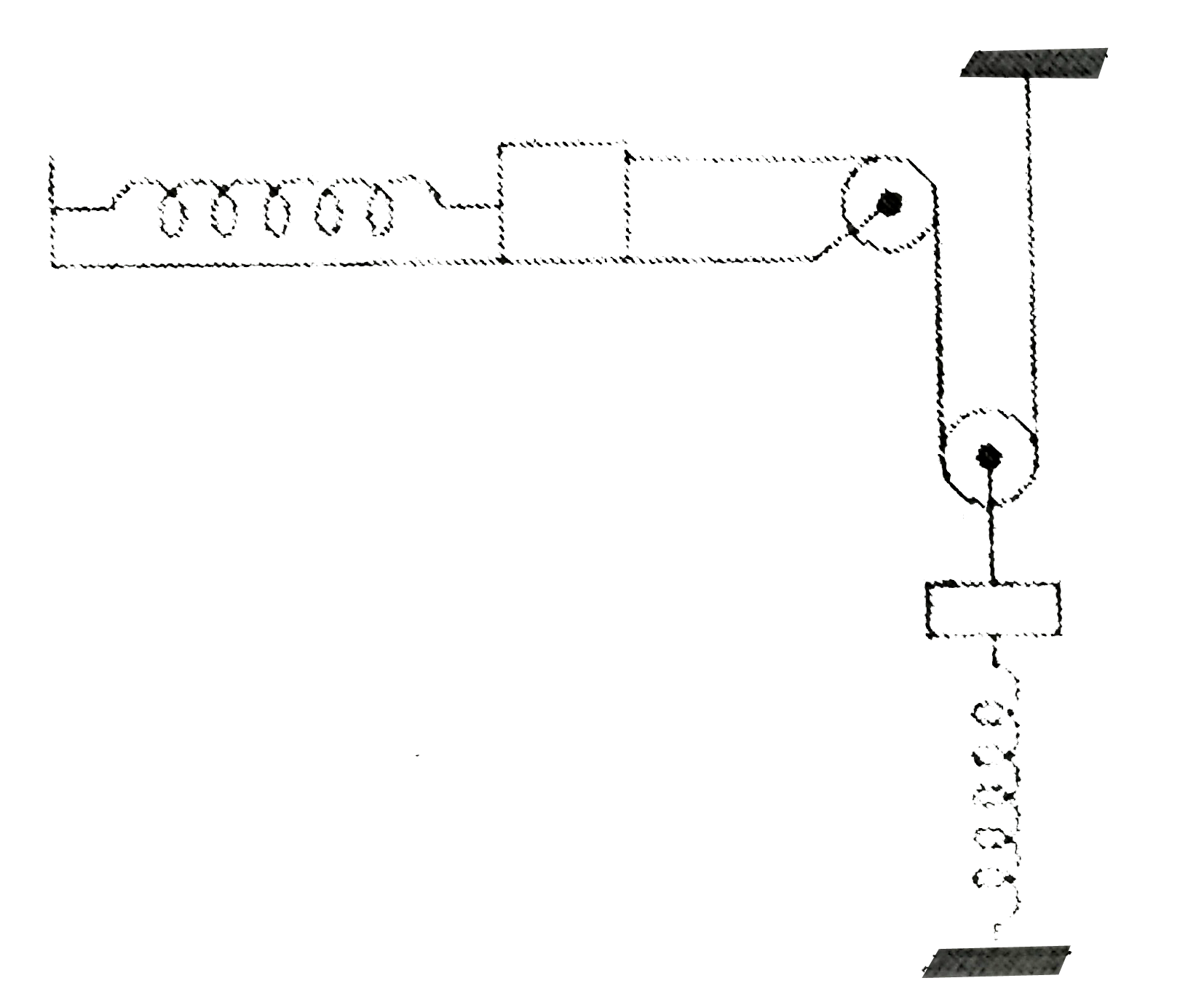
In the equilibrium position, speed of the block placed horizontally is
3.21m/s
2.21m/s
1.93m/s
1.26m/s
The correct Answer is:D
Step by step video, text & image solution for The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m. In the equilibrium position, speed of the block placed horizontally is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:D Matrix Matching Type Questions
Explore 10 Videos
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:E Integer Type Questions
Explore 11 Videos
- WORK, POWER AND ENERGYBook:DC PANDEYChapter:WORK, POWER AND ENERGYExercise:B More than One Option is Correct
Explore 26 Videos
- WORK, ENERGY AND POWERBook:DC PANDEYChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
In the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
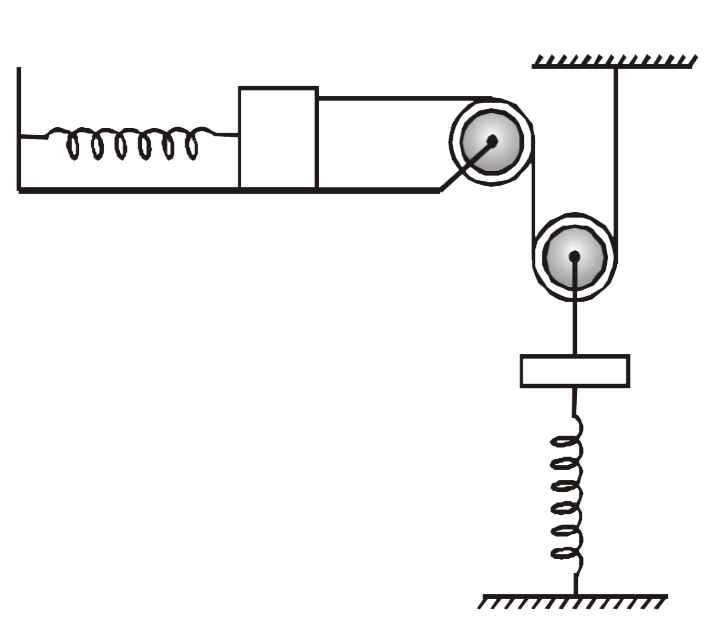
Maximum speed of the block placed horizontally is:
View SolutionA 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
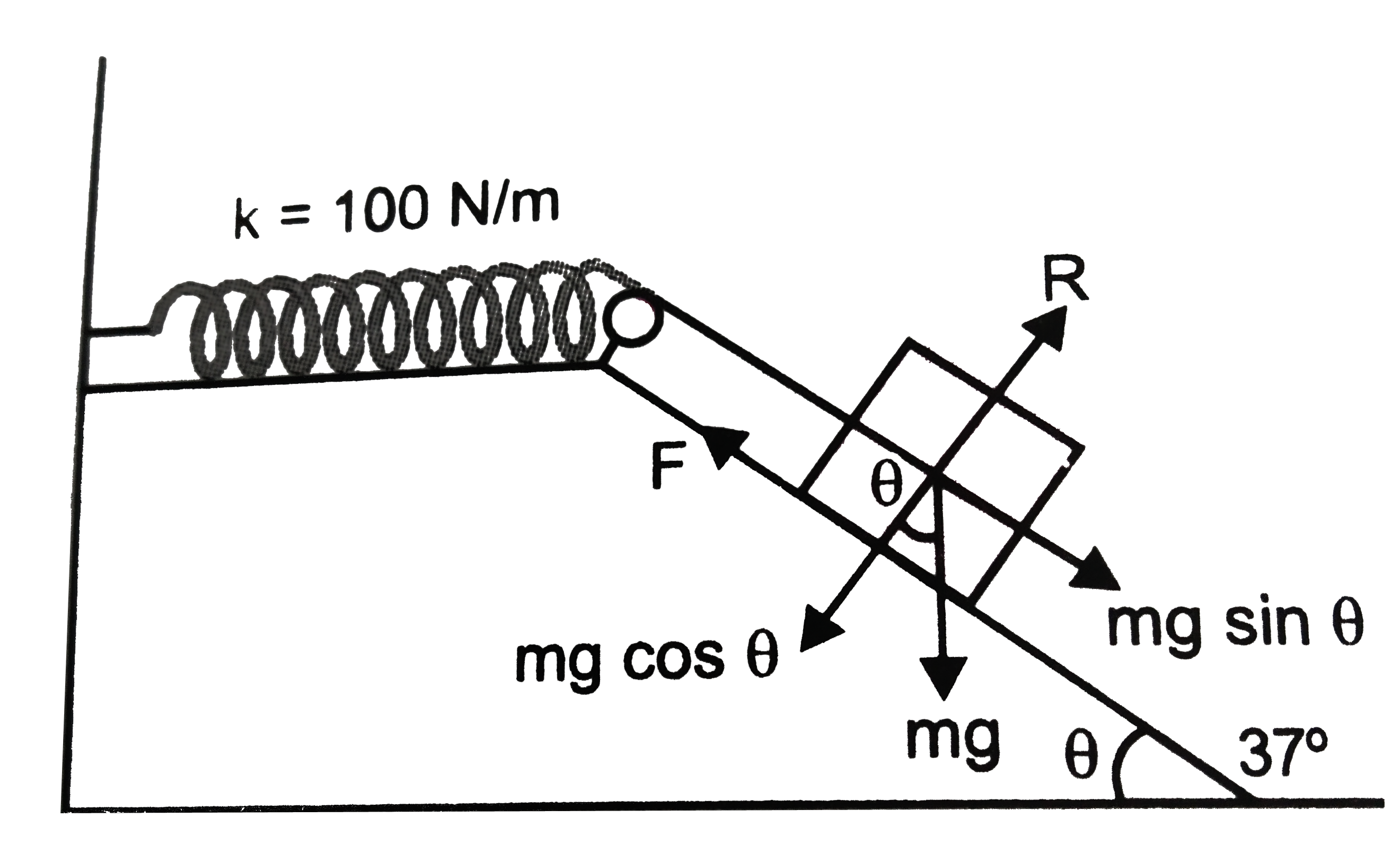
View Solution
Knowledge Check
The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
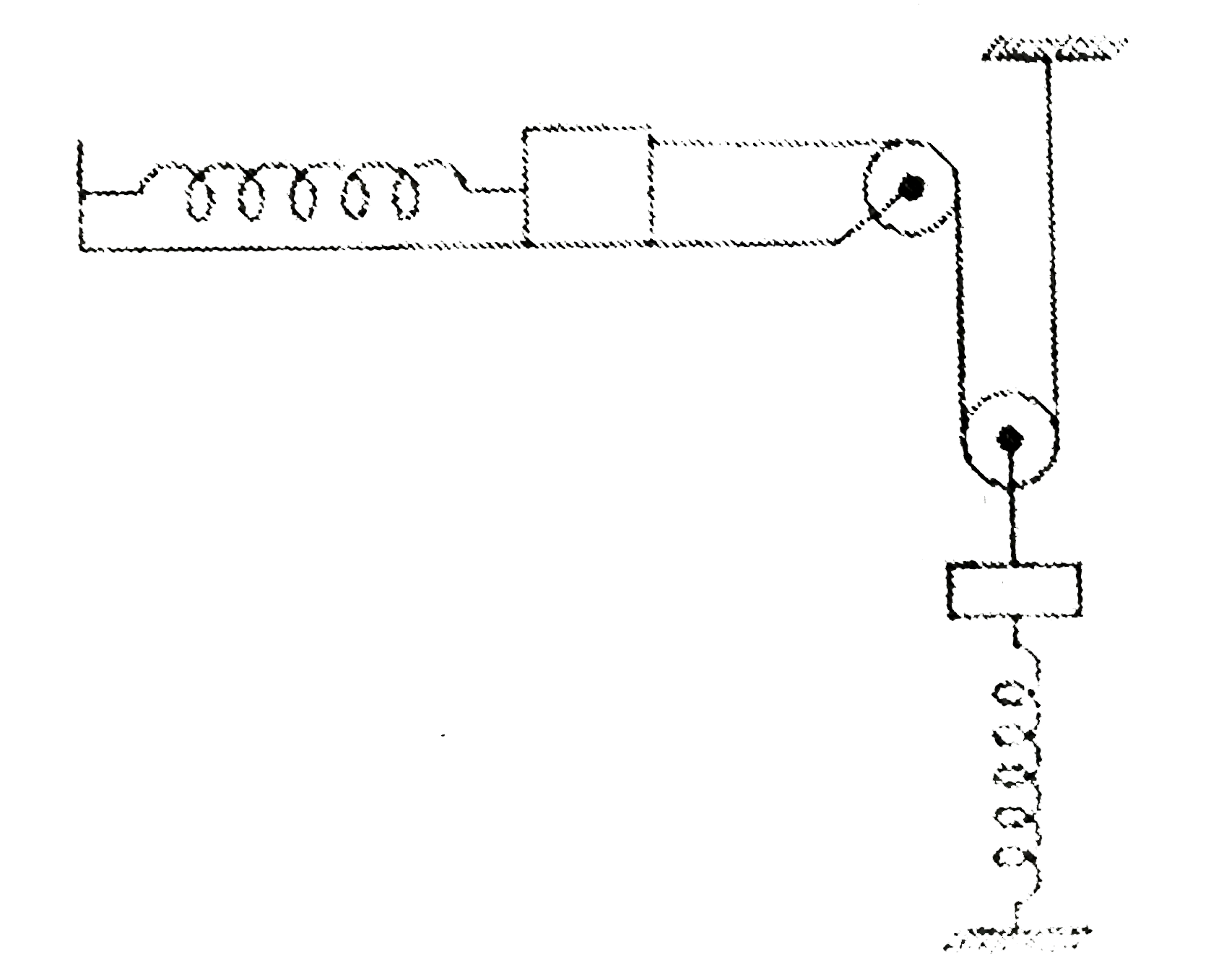
Extension of horizontal spring in equilibrium isA0.2 mB0.4 mC0.6 mD0.8 mThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m. Extension of horizontal spring in equilibrium is:
 A0.2mB0.4mC0.6mD0.8m
A0.2mB0.4mC0.6mD0.8mThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1kg and force constant of each spring is 10N/m. Then choose the incorrect option(s). Assume puleys and strings are massless and all contacts are smooth. (g=10m/s2)
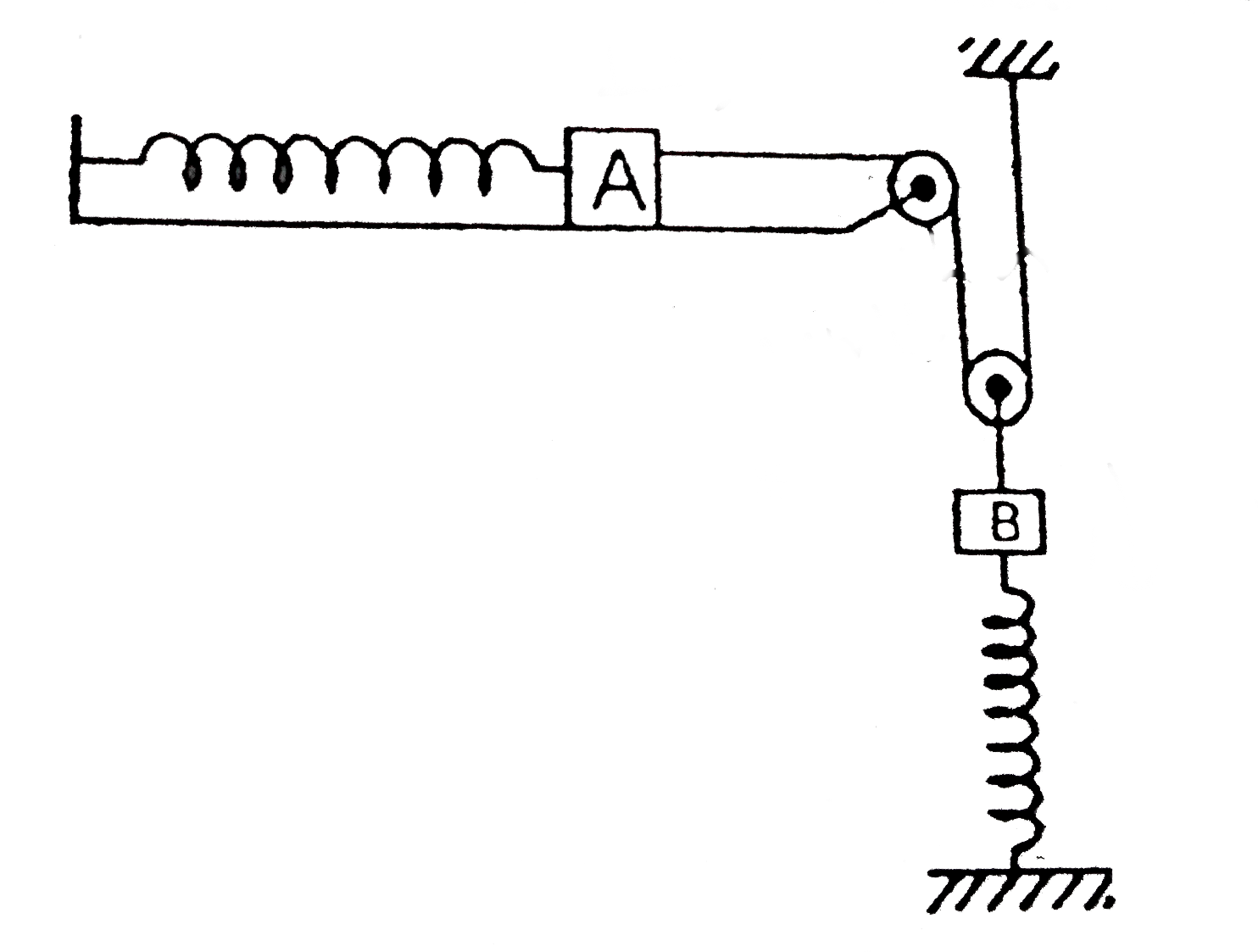 AExtension of horizontal spring in spring in equilibrium is 0.4mBExtension of horizontal spring in spring in equilibrium is 0.2mCMaximum speed of the block A is 8m/sDMaximum speed of the block A is 12m/s
AExtension of horizontal spring in spring in equilibrium is 0.4mBExtension of horizontal spring in spring in equilibrium is 0.2mCMaximum speed of the block A is 8m/sDMaximum speed of the block A is 12m/s
Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
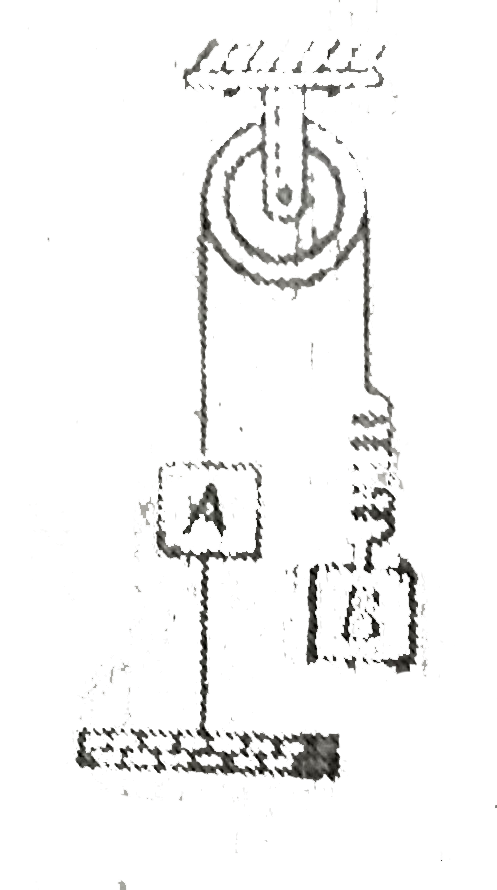
View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
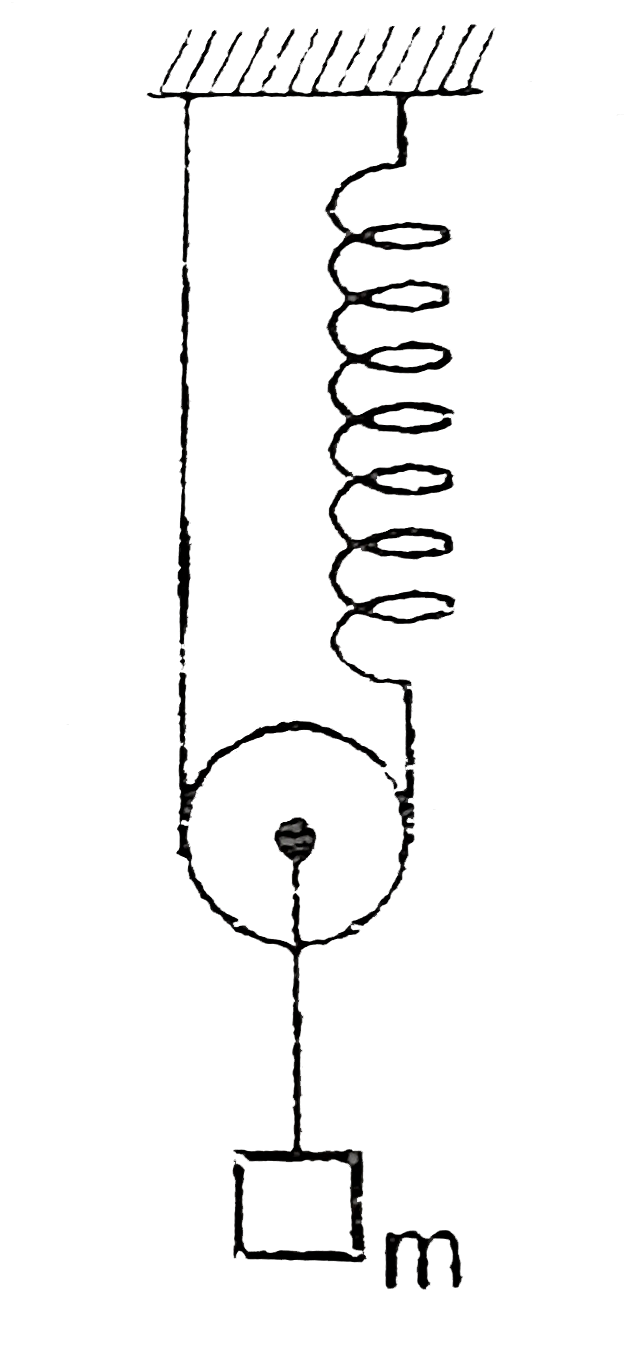
View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
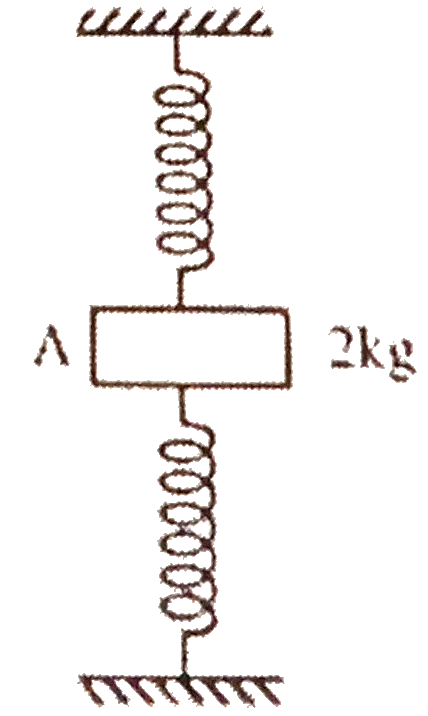
View SolutionA block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
View Solution

