Three mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring. When is 0.4 kg mass is removed , the system oscillates with a period 2 s . When the 0.3 kg mass is also removed , the system will oscillates with a period
1 s
2 s
3 s
4 s
The correct Answer is:A
To solve the problem step by step, we will determine the period of oscillation when the 0.3 kg mass is also removed from the spring-mass system.
1. Identify the initial conditions:
- We have three masses: m1=0.1kg, m2=0.3kg, and m3=0.4kg.
- When the 0.4 kg mass is removed, the remaining mass is m1+m2=0.1kg+0.3kg=0.4kg.
2. Use the formula for the period of a spring-mass system:
The period T of a mass-spring system is given by:
T=2π√mk
where m is the mass and k is the spring constant.
3. Set up the equation for the first scenario:
- When the 0.4 kg mass is removed, the period is given as T=2s.
- Thus, we have:
2=2π√0.4k
- Dividing both sides by 2π:
1π=√0.4k
- Squaring both sides:
1π2=0.4k
- Rearranging gives:
k=0.4π2
4. Set up the equation for the second scenario:
- Now, we need to find the period when the 0.3 kg mass is also removed, leaving only the 0.1 kg mass.
- The new mass m=0.1kg.
5. Calculate the new period:
- Using the same formula for the period:
T=2π√0.1k
- Substituting k=0.4π2:
T=2π√0.10.4π2
- Simplifying:
T=2π√0.10.4⋅1π=2√0.10.4=2√14=2⋅12=1s
6. Conclusion:
- The period of oscillation when the 0.3 kg mass is also removed is T=1s.
Final Answer:
The period of oscillation when the 0.3 kg mass is also removed is 1 second.
- We have three masses: m1=0.1kg, m2=0.3kg, and m3=0.4kg.
- When the 0.4 kg mass is removed, the remaining mass is m1+m2=0.1kg+0.3kg=0.4kg.
The period T of a mass-spring system is given by:
T=2π√mk
where m is the mass and k is the spring constant.
- When the 0.4 kg mass is removed, the period is given as T=2s.
- Thus, we have:
2=2π√0.4k
- Dividing both sides by 2π:
1π=√0.4k
- Squaring both sides:
1π2=0.4k
- Rearranging gives:
k=0.4π2
- Now, we need to find the period when the 0.3 kg mass is also removed, leaving only the 0.1 kg mass.
- The new mass m=0.1kg.
- Using the same formula for the period:
T=2π√0.1k
- Substituting k=0.4π2:
T=2π√0.10.4π2
- Simplifying:
T=2π√0.10.4⋅1π=2√0.10.4=2√14=2⋅12=1s
- The period of oscillation when the 0.3 kg mass is also removed is T=1s.
The period of oscillation when the 0.3 kg mass is also removed is 1 second.
Similar Questions
Three masses of 500g, 300g and 100g are suspended at the end of a spring as shown and are in equilibrium. When the 500g mass is removed suddenly, the system oscillates with a period of 2s. When the 300g mass is also removed, it will oscillate with period T. Find the value of T.
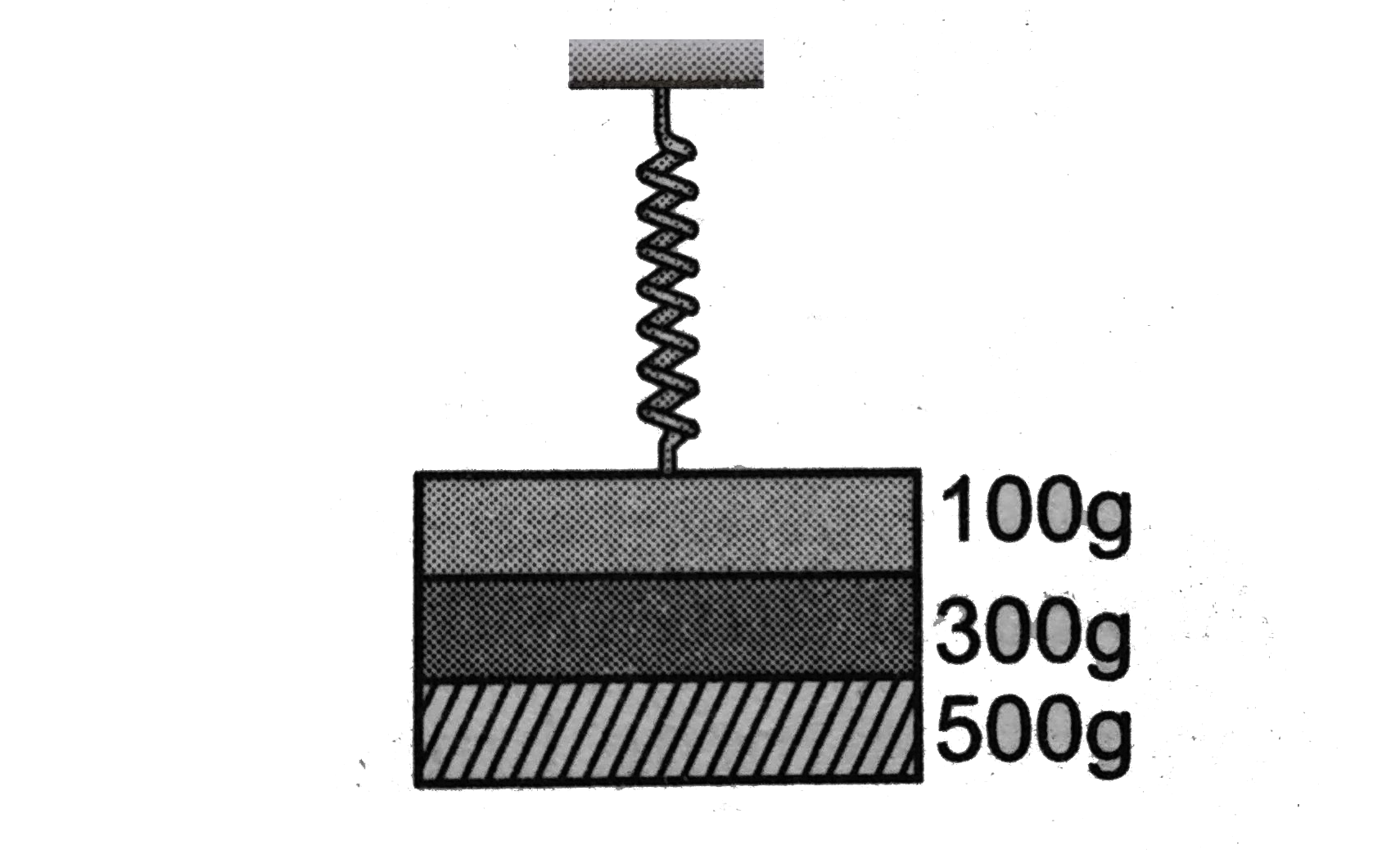
View SolutionThree masses 700g, 500g, and 400 g are suspended at the end of a spring a shown and are in equilibrium. When the 700 g mass is removed, the system oscillacts with a period of 3 seconds, when the 500 gm mass is also removed, it will oscillate with a period of

View SolutionWhen a mass of 5 kg is suspended from a spring of negligible mass and spring constant K, it oscillates with a periodic time 2π. If the mass is removed, the length of the spring will decrease by
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
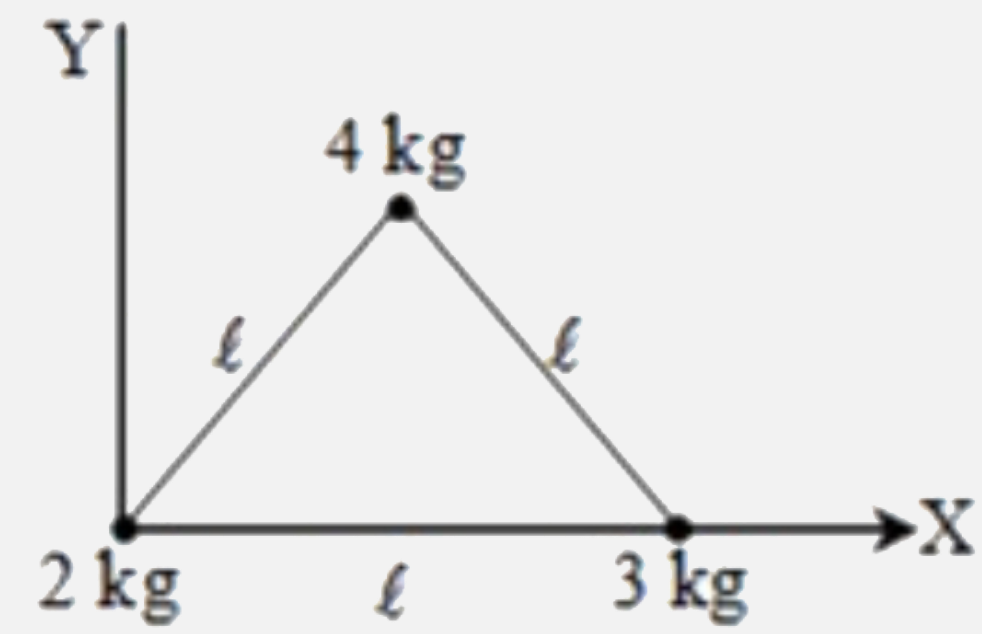
View SolutionThree masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
View SolutionTwo masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system . The amplitude of oscillation is
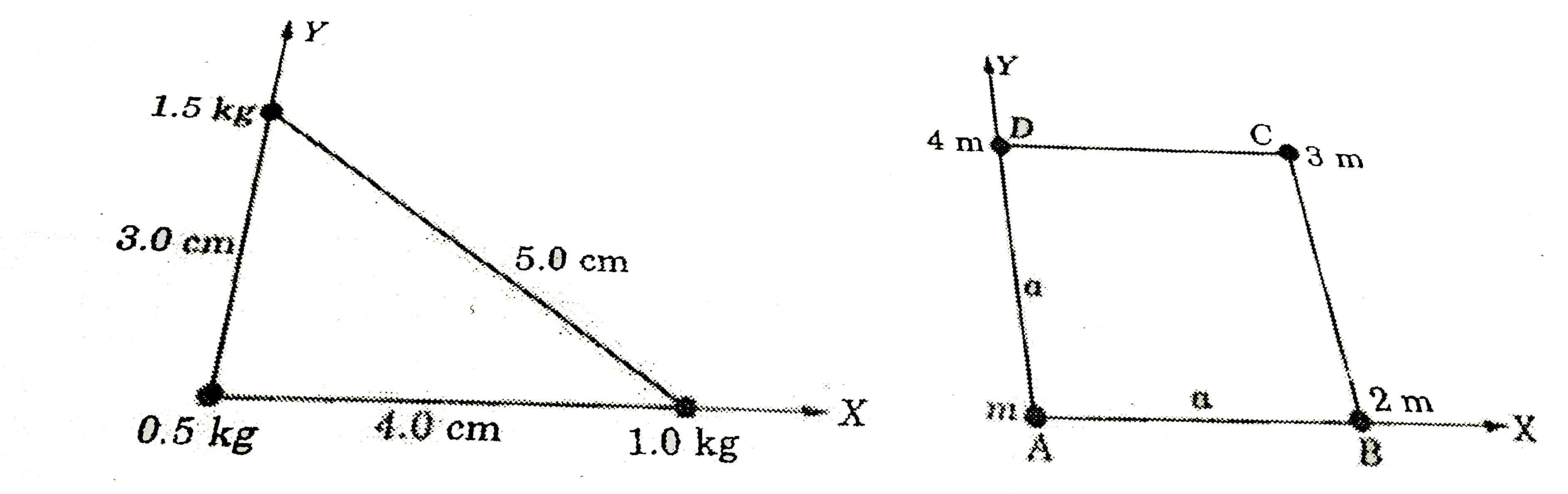
View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View SolutionTwo masses m1=1kgandm2=0.5kg are suspended together by a massless spring of spring constant 12.5Nm−1. When masses are in equilibrium m1 is removed without disturbing the system. New amplitude of oscillation will be
View Solution