Question

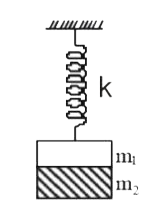
Two masses 8 kg 4 kg are suspended together by a massless spring of spring constant $1000N{m}^{-1}$ . When the masses are in equilibrium 8 kg is removed without disturbing the system . The amplitude of oscillation is

Options

A. 0.5 m
B. 0.08 m
C. 0.4 m
D. 0.04 m

Answer

B

Explanation

To solve the problem step by step, we will analyze the situation where two masses (8 kg and 4 kg) are suspended from a spring, and then we will determine the amplitude of oscillation after removing the 8 kg mass.

Step 1: Calculate the total weight of the system before removing the 8 kg mass.
The total weight (W) of the two masses when both are suspended is given by:
\( W = (m_1 + m_2) \cdot g \)
where \( m_1 = 8 \, \text{kg} \), \( m_2 = 4 \, \text{kg} \), and \( g = 10 \, \text{m/s}^2 \) (approximating gravitational acceleration).

\( W = (8 + 4) \cdot 10 = 12 \cdot 10 = 120 \, \text{N} \)

Step 2: Determine the extension of the spring when both masses are attached.
Using Hooke's Law, the extension \( x_1 \) of the spring can be calculated using:
\( F = k \cdot x \)
where \( F \) is the total weight and \( k \) is the spring constant.

Given \( k = 1000 \, \text{N/m} \):
\( 120 = 1000 \cdot x_1 \)
\( x_1 = \frac{120}{1000} = 0.12 \, \text{m} \)

Step 3: Calculate the weight of the remaining mass after removing the 8 kg mass.
After removing the 8 kg mass, only the 4 kg mass remains. The weight of the remaining mass \( W' \) is:
\( W' = m_2 \cdot g = 4 \cdot 10 = 40 \, \text{N} \)

Step 4: Determine the new extension of the spring with only the 4 kg mass.
Using Hooke's Law again for the remaining mass:
\( 40 = 1000 \cdot x_2 \)
\( x_2 = \frac{40}{1000} = 0.04 \, \text{m} \)

Step 5: Calculate the amplitude of oscillation.
The amplitude of oscillation \( A \) is the difference in extension of the spring before and after removing the 8 kg mass:
\( A = x_1 - x_2 = 0.12 - 0.04 = 0.08 \, \text{m} \)

Final Answer:
The amplitude of oscillation is \( 0.08 \, \text{m} \).

---