Fig. shows two vertical forces and a couple of moment 2000 Nm acting on a horizontal rod which is fixed at end A. 1. Determine the resultant of the system 2. Determine an equivalent system through A.
i Resultant of the system ∑V = –4000 + 2500 = –1500 N R = ∑V21/2 = 1500 N acting downwards for finding the position of the resultant apply varignon’s theorem i.e Moment of resultant = sum of moment of all the forces about any point. Let from point be A and distance of resultant is ‘d’ m from A R.d = 4000 × 1 + 2000 – 2500 × 2.5 -1500 × d = -250 ⇒ d = 0.166 m from point A ii Equivalent system through A Equivalent system consist of: 1. A single force R passing through the given point and 2. A single moment ∑M Where R = the resultant of all force acting on the body ∑M = Sum of all moments of all the forces about point A. Hence single force is = 1500 N; And couple = 250 Nm.
Related Solutions
A couple is acting on a two particle system. The resultant motion will be:
View SolutionA couple is acting on a two particle system. The resultant motion will be
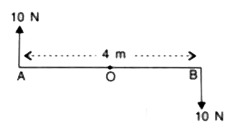
View SolutionThe forces each of magnitude 10N act vertically upwards and downwards respectively at the two ends A and B of a uniform rod of length 4m which is pivoted at its mid point O as shown is fig. 1.30, Determine the magnitude of the resultant moment of forces about the pivot O.
View SolutionThree charges q, -2q and q are placed at three vertices of an equilateral triangle. Determine the equivalent dipole moment of the system.
View SolutionTwo forces, each of magnitude 3 N, act vertically in opposite direction at the two ends of a uniform rod of length 1 m, pivoted at its centre. Draw a diagram of the arrangement and determine the resultant moment of the forces about the mid-point of the rod.
View SolutionTwo forces each of magnitude 2N act vertically upwards and downwards respectively at the two ends of a uniform rod of length 1m which is pivoted at its centre. Draw a diagram of the arrangement and determine the resultant moment of forces about the mid point of the rod.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
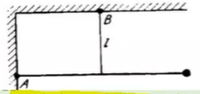
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).

The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).

The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA rod can turn freely about one of its ends which is fixed. At the other end a horizontal force equal to half the weight of the rod is acting. In the position of equilibrium, the rod is inclined to the vertical at an angle
View SolutionTwo identical weightless rods are hinged to each other and to a horizontal beam (Fig.). The rigidity of each rod is , and the angle between them is . Determine the rigidity k of the system of rods relative to the vertical displacement of a hinge A under the action of a certain force F, assuming that displacements are small in comparison with the length of the rods.

View SolutionIf resultant of forces acting on a system is zero then
View SolutionDetermine the point of application of force, when forces are acting on the rod as shown in figure.[here 10N force make 37° with horizontal]
View SolutionStatement-1: If the resultant of all the forces acting on a system is zero then the torque on the system about any point is same. Statement-2: If the resultant of the forces acting on a system is zero then acceleration of its centre of mass is zero.
View SolutionDetermine the point of application of resultant force, when forces acting on the rod are as shown in figure.
View SolutionFig. shows a ball having a charge q fixed at a point A. Two identical balls of mass m having charge are attaached to the end of a light rod of length 2a. The system is released from the situation shown in fig. Find the angular velocity of the rod when the rod turns through
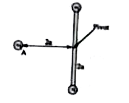
View SolutionFig. shows a ball having a charge q fixed at a point A. Two identical balls of mass m having charge are attaached to the end of a light rod of length 2a. The system is released from the situation shown in fig. Find the angular velocity of the rod when the rod turns through

View SolutionDetermine the point of application of force, when forces are acting on the rod as shown in figure.
View SolutionA horizontal force of magnitude Facts at the end of a uniform rigid rod which is welded at point . In each case and , as shown in Fig., find the reaction. force acting at a point at a distance from the fixed end of the rod.
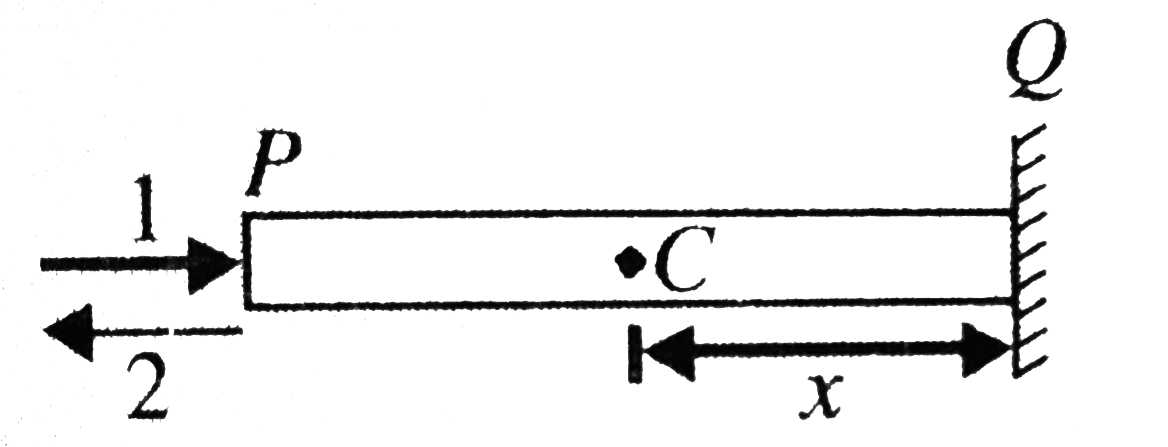
View SolutionA horizontal force of magnitude Facts at the end P of a uniform rigid rod which is welded at point Q . In each case 1 and 2 , as shown in Fig., find the reaction. force acting at a point C at a distance x from the fixed end Q of the rod.
View Solution