A rod can turn freely about one of its ends which is fixed. At the other end a horizontal force equal to half the weight of the rod is acting. In the position of equilibrium, the rod is inclined to the vertical at an angle
30∘
45∘
60∘
None
The correct Answer is:B
To solve the problem of the rod in equilibrium, we will analyze the forces and torques acting on the rod.
1. Identify the Forces Acting on the Rod:
- Let the weight of the rod be W.
- A horizontal force F is acting at the free end of the rod, where F=12W.
2. Determine the Position of the Center of Mass:
- The center of mass of the rod is located at its midpoint, which is at a distance of L2 from the pivot point (the fixed end).
3. Set Up the Torque Equation:
- The torque due to the weight of the rod (acting downwards at the center of mass) is given by:
τweight=W⋅(L2⋅cos(θ))
- The torque due to the horizontal force F is given by:
τforce=F⋅(L⋅sin(θ))
- Since F=12W, we can substitute this into the torque equation:
τforce=(12W)⋅(L⋅sin(θ))
4. Equate the Torques for Equilibrium:
- For the rod to be in equilibrium, the clockwise torque must equal the anticlockwise torque:
W⋅(L2⋅cos(θ))=(12W)⋅(L⋅sin(θ))
5. Simplify the Equation:
- Cancel W and L from both sides (assuming W and L are non-zero):
12cos(θ)=12sin(θ)
- This simplifies to:
cos(θ)=sin(θ)
6. Solve for the Angle θ:
- The equation cos(θ)=sin(θ) implies that:
tan(θ)=1
- Therefore, the angle θ is:
θ=45∘
Final Answer:
The rod is inclined to the vertical at an angle of 45∘.
- Let the weight of the rod be W.
- A horizontal force F is acting at the free end of the rod, where F=12W.
- The center of mass of the rod is located at its midpoint, which is at a distance of L2 from the pivot point (the fixed end).
- The torque due to the weight of the rod (acting downwards at the center of mass) is given by:
τweight=W⋅(L2⋅cos(θ))
- The torque due to the horizontal force F is given by:
τforce=F⋅(L⋅sin(θ))
- Since F=12W, we can substitute this into the torque equation:
τforce=(12W)⋅(L⋅sin(θ))
- For the rod to be in equilibrium, the clockwise torque must equal the anticlockwise torque:
W⋅(L2⋅cos(θ))=(12W)⋅(L⋅sin(θ))
- Cancel W and L from both sides (assuming W and L are non-zero):
12cos(θ)=12sin(θ)
- This simplifies to:
cos(θ)=sin(θ)
- The equation cos(θ)=sin(θ) implies that:
tan(θ)=1
- Therefore, the angle θ is:
θ=45∘
The rod is inclined to the vertical at an angle of 45∘.
Similar Questions
A uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View Solution
Knowledge Check
A rod is hinged vertically at one end and is forced to oscillate in a vertical plane with hinged end at the top, the motion of the rod:
Ais simple harmonicBis oscillatory but not simple harmonicCis pericolic but not oscillatoryDmay be simple harmonicA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
A(l2−a2)/a2B(l2−a2)/2a2C(l2−a2)/3a2Dnone of theseA disk is fixed at its centre O and rotating with constant angular velocity ω. There is a rod whose one end is connected at A on the disc and the other end is connected with a ring which can freely moce along the fixed vertical smooth rod. At an instant when the rod is making an angle 30∘ with the vertical the ring is found to have a velocity v in the upward direction. Find ω of the disk. Given that the point A is R/2 distance above point O and length of the rod Ab is l
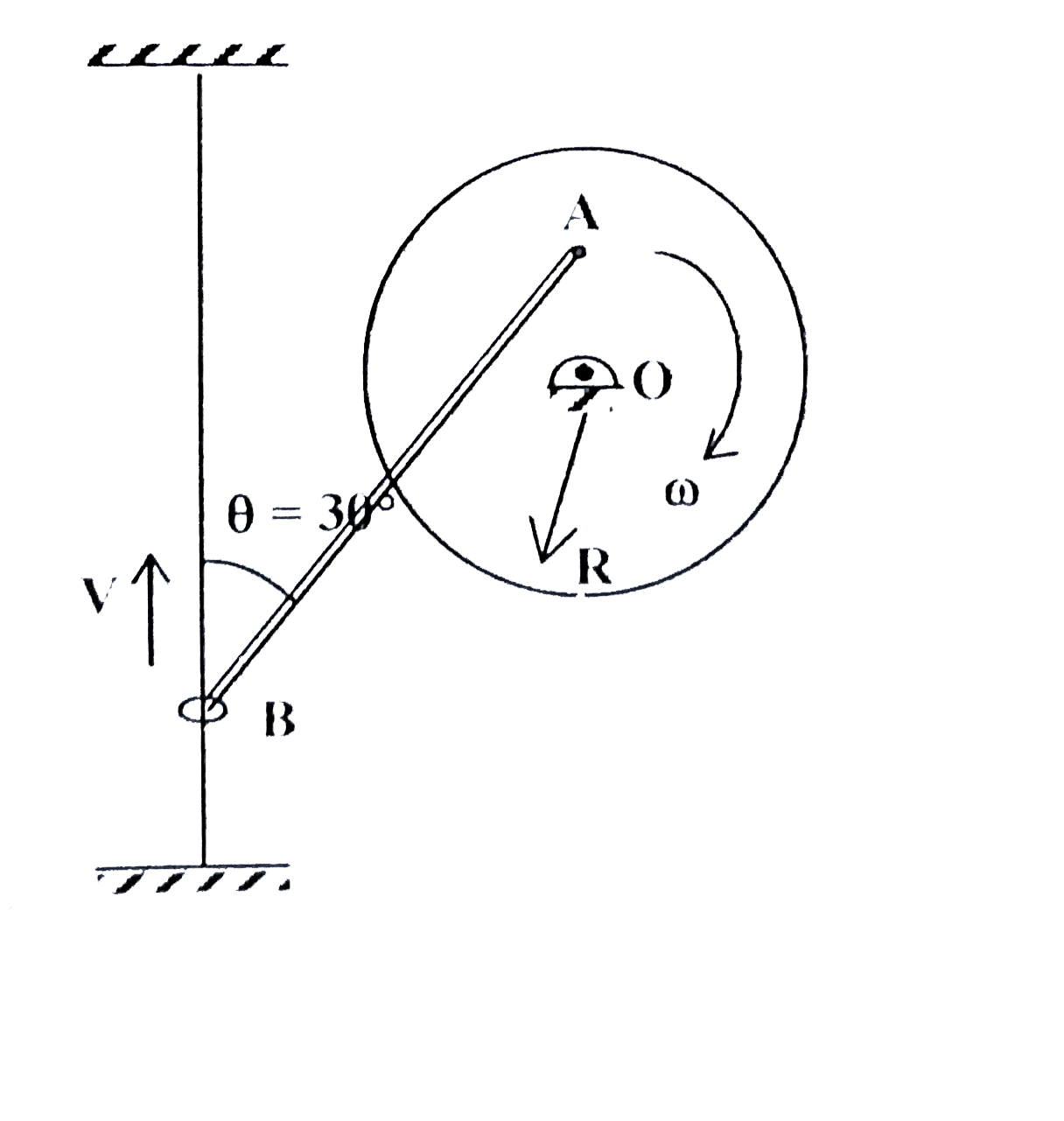 Av√32lBv√32RC2√3vRD2vl√3
Av√32lBv√32RC2√3vRD2vl√3
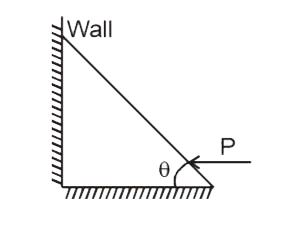
Assuming frictionless contacts, determine the magnitude of external horizontal force P applied at the lower end for equilibrium of the rod. The rod is uniform and its mass is 'm'.
View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
View SolutionA uniform rod of mass M and length L is hinged at its lower end on a table. The rod can rotate freely in vertical plane and there is no friction at the hinge. A ball of mass M and radius R=L3 is placed in contact with the vertical rod and a horizontal force F is applied at the upper end of the rod.
(a) Find the acceleration of the ball immediately after the force starts acting.
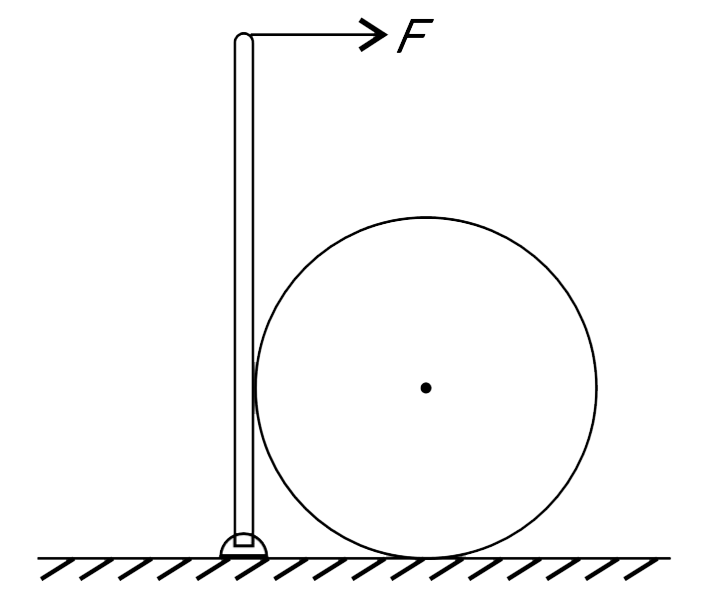
(b) Find the horizontal component of hinge force acting on the rod immediately after force F starts acting.
View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View Solution

