A rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

The fall in postion of the CM of the rod, h=12(1−cosθ)
In the process, decrease in E is equal to increase in rotational
KE of the rod, so mgh=12Iω2
or mg12(3gl(1−cosθ))
The velocity of the CM of the rod VCM=ωr is
√3gl(1−cosθ)×l2=√3gl(1−cosθ)4
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View Solution
Knowledge Check
A slender rod of mass m and length L is pivoted about a horizontal axis through one end and released from rest at an angle of 30∘ above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is
 A√104 mg along horizontalBmg along verticalC√104mg alonng a line making an angle of tan−1(13) with the horizontalD√104mg along a line making an angle of tan−1(3) with the horizontal
A√104 mg along horizontalBmg along verticalC√104mg alonng a line making an angle of tan−1(13) with the horizontalD√104mg along a line making an angle of tan−1(3) with the horizontalA rod of length L whose lower end is fixed along the horizontal plane starts to topple from the vertical position. The velocity of the upper end of the rod when it hits the ground is
A√3gLB√2gLC√gLD√5gLIn the above problem, if the rod is released from horizontal position, the angular velocity of the rod as it passes the vertical position is (l=length fo rod)
A√12g5lB√2g3lC√3glD√3g7l
A uniform rod is rotating about a horizontal axis as shown. The rod is hinged at one of the ends. The rod is released from a vertical position by slightly pushing it. As the rod moves from A to B
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View SolutionA rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View Solution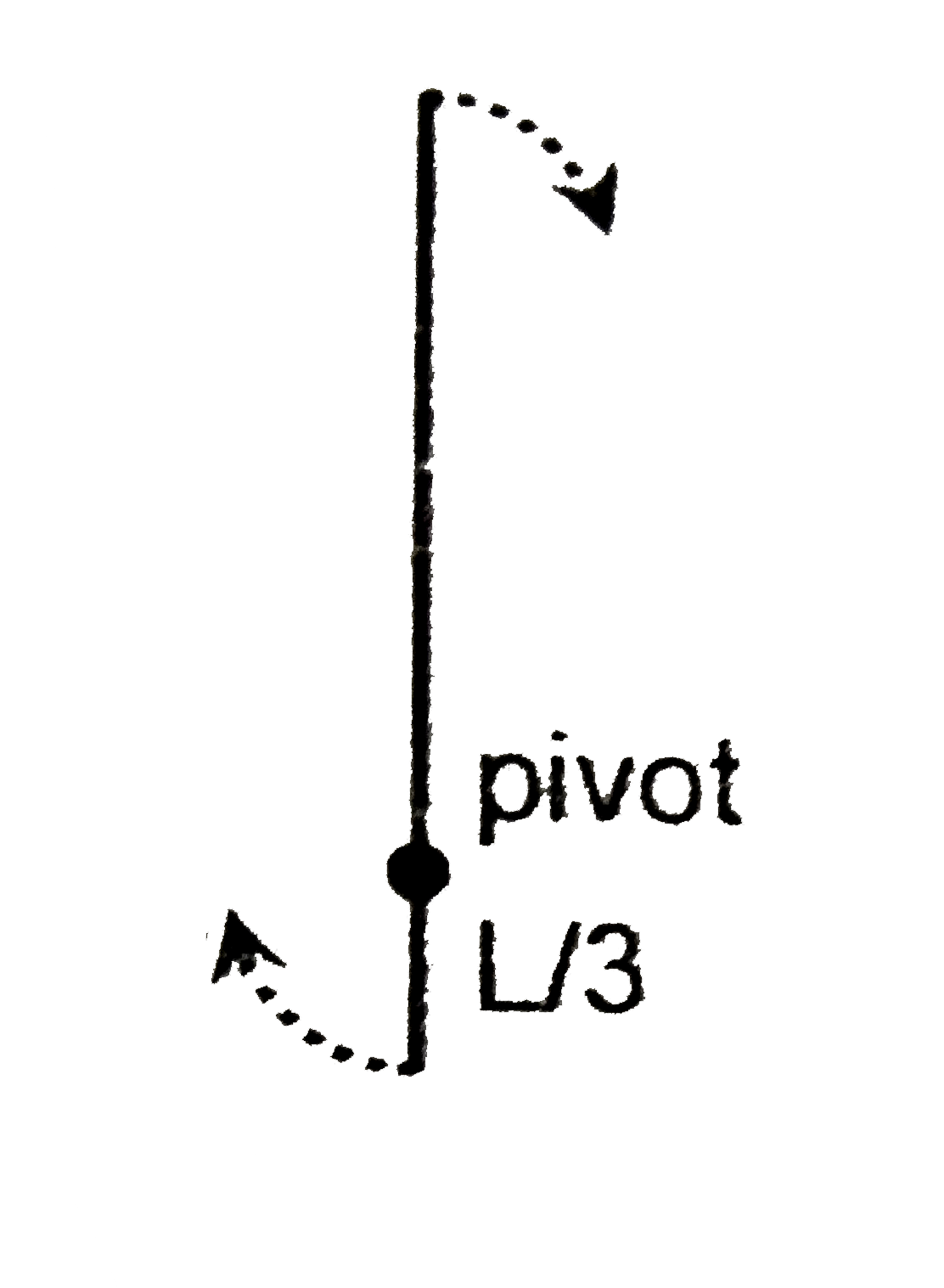
A uniform rod of mass M and length L is free to rotate about a frictionless pivot located L/3 from one end. The rod is released from rest incrementally away from being perfectly vertical, resulting in the rod rotating clockwise about the pivot. when the rod is horzontal what is the magnitude of the tangential acceleration of its center of mass?
View Solution

