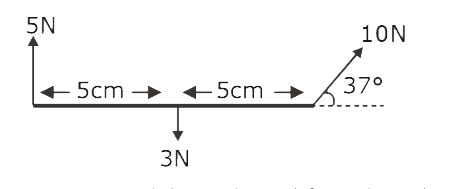
Determine the point of application of force, when forces are acting on the rod as shown in figure.[here 10N force make 37° with horizontal]
![Determine the point of application of force, when forces are acting on the rod as shown in figure.[here 10N force make 37° with horizontal]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MOT_CON_NEET_PHY_C15_SLV_037_Q01.png)
Video Solution
Text Solution
Since the body is in equillibrium so we conclude →F≠t=0 and torque about any point is zero i.e.,
→taru≠t=0
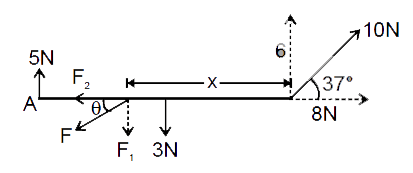
Let us assume that we apply F force downward at A angle from the horizontal, at x distance from B
From →F≠t=0
⇒ Fnetx=0 which gives
F2=8N
From Fnet y=0⇒5+6=F1+3
⇒ F1=8N
If body is in equillibrium then torque about point B is zero.
⇒ 3×5+F1x−5×10=0
⇒ 15+18x−50=0
x=359
|
Topper's Solved these Questions
- ROTATIONAL MOTION Book:MOTIONChapter:ROTATIONAL MOTION Exercise:Exercise - 1
Explore 90 Videos
- ROTATIONAL MOTION Book:MOTIONChapter:ROTATIONAL MOTION Exercise:Exercise - 2
Explore 40 Videos
- RAY OPTICSBook:MOTIONChapter:RAY OPTICSExercise:Exercise-4
Explore 38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBook:MOTIONChapter:SEMI CONDUCTOR AND LOGIC GATESExercise:EXERCISE 3
Explore 34 Videos
Similar Questions
Knowledge Check
Determine the point of application of force, when forces of 20N and 30N are acting on rod as shown in figure.
 A70 mB80 mC60 mD50 m
A70 mB80 mC60 mD50 mTwo forces F1 and F2 are acting on a rod abc as shown in figure.
 Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)
Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)As shown in the figure , the friction force acting on the block is
 A50NB30NC20NDNone
A50NB30NC20NDNone
Draw normal forces on the massive rod at point 1 and 2 as shown in figure.
View SolutionDraw normal forces on the massive rod at point 1 and 2 as shown in figure.
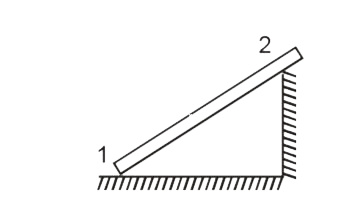
View SolutionA wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.

View SolutionA force F is acted on a body as shown in the figure. Find the impulse of the force in first four seconds.

View SolutionA block of mass 10kg is displaced by 10m towards right by the application of force F=20N( 60 from horizontal ), as shown in the figure. The work done by the force is
View Solution