A solid uniform sphere of radius R and mass M rolls without slipping with angular velocity w0 when it encounters a step of height 0.4 R. Find the angular velocity immediately after inelastic impact with the rough step.
Applying conservatio principle of angular momentum about point of impact
Related Solutions
A sphere of mass m and radius r rolls without slipping on the horizontal surface with speed v . During its motion it encounters a fixed rectangular block of height h=(r )/(4) as shown. The collision is inelastic. Find the angular speed of sphere immediately after collision. The body rolls without slipping.
View SolutionA uniform solid sphere of mass m, radius R moving with velocity is rolling without slipping on a frictionless surface vertical wall. Ratio of magnitude of angular momentum of the sphere and after the collision about its bottommost point is
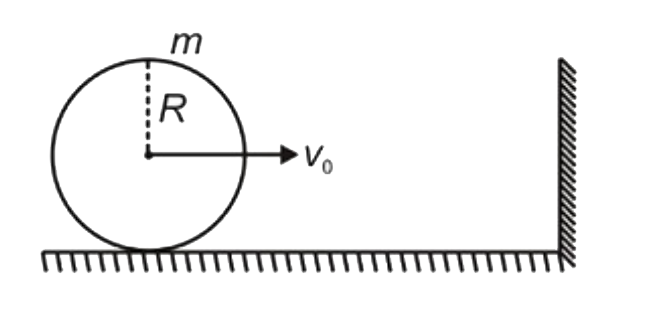
View SolutionA uniform solid sphere of mass m, radius R moving with velocity is rolling without slipping on a frictionless surface vertical wall. Ratio of magnitude of angular momentum of the sphere and after the collision about its bottommost point is

View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.
View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.
View SolutionA solid sphere is rolling on a rough surface, whose centre of mass is at C at a certain instant. Find at that instant it has angular velocity omega . Its radius is R . Find the angular acceleration at that instant mass of sphere is m
View SolutionA solid sphere is rolling on a rough surface, whose centre of mass is at C at a certain instant. Find at that instant it has angular velocity omega . Its radius is R . Find the angular acceleration at that instant mass of sphere is m
View SolutionA uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA uniform ball of radius rolls without slipping down from the top of a sphere of radius Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution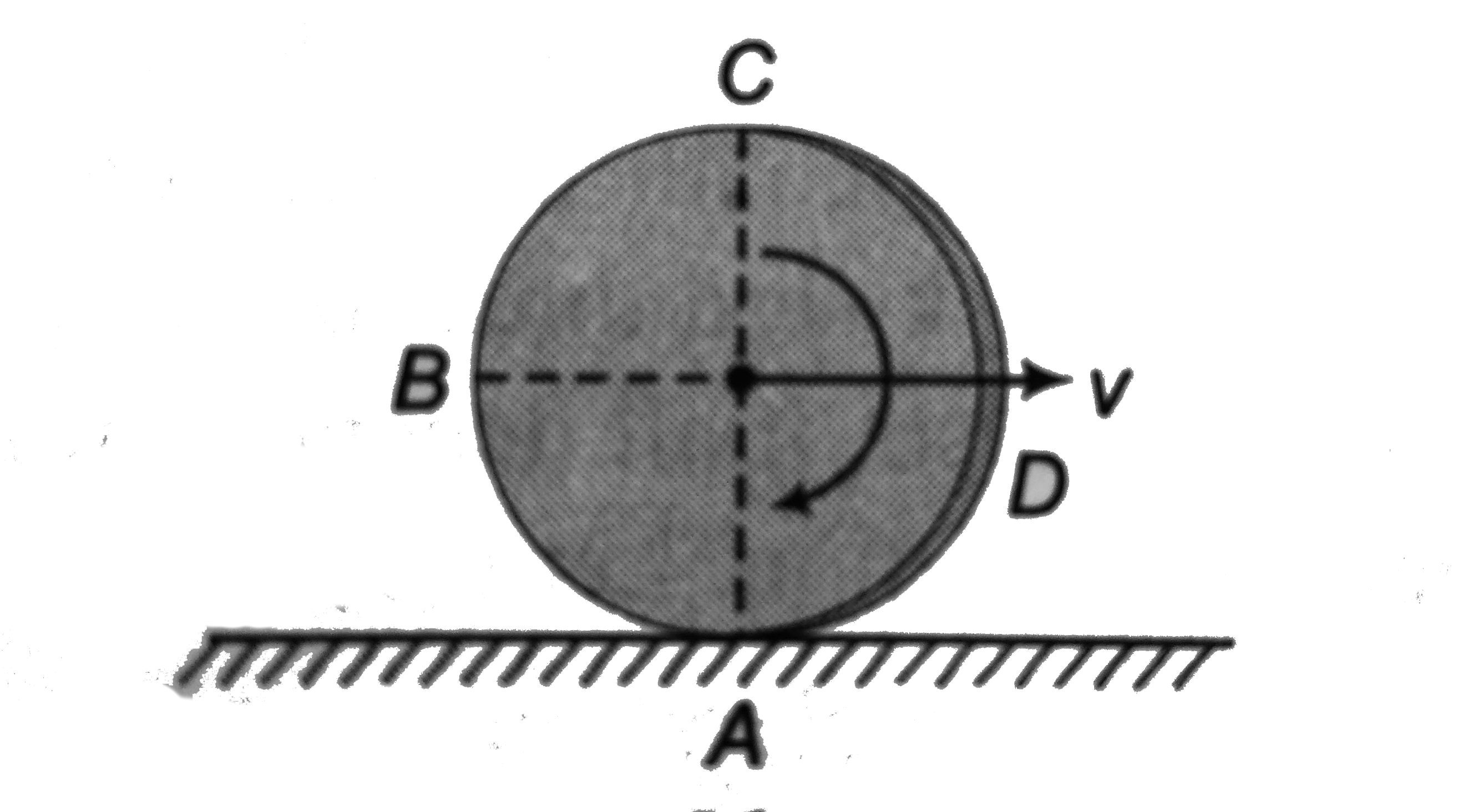
A solid sphere of mass and radius is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA solid sphere is rolling on a rough surface without slipping and the speed of the center of mass v_(0) If the mass of the sphere is m and the radius R is fixed, then find the angular momentum of the sphere with respect to the point of contact.
View SolutionA uniform sphere of mass and radius is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when .
View SolutionA uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v_(0) and angular omega_(0) = (2v_(0))/(R ) and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction mu = 2 tan theta as shown. The time after which the sphere will start rolling without slipping is
View SolutionA uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v_(0) and angular omega_(0) = (2v_(0))/(R ) and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction mu = 2 tan theta as shown. The time after which the sphere will start rolling without slipping is
View SolutionA sphere of radius rolls without slipping between two planks as shown in figure. Find
Speed of centre of sphere
Angular velocity of the sphere
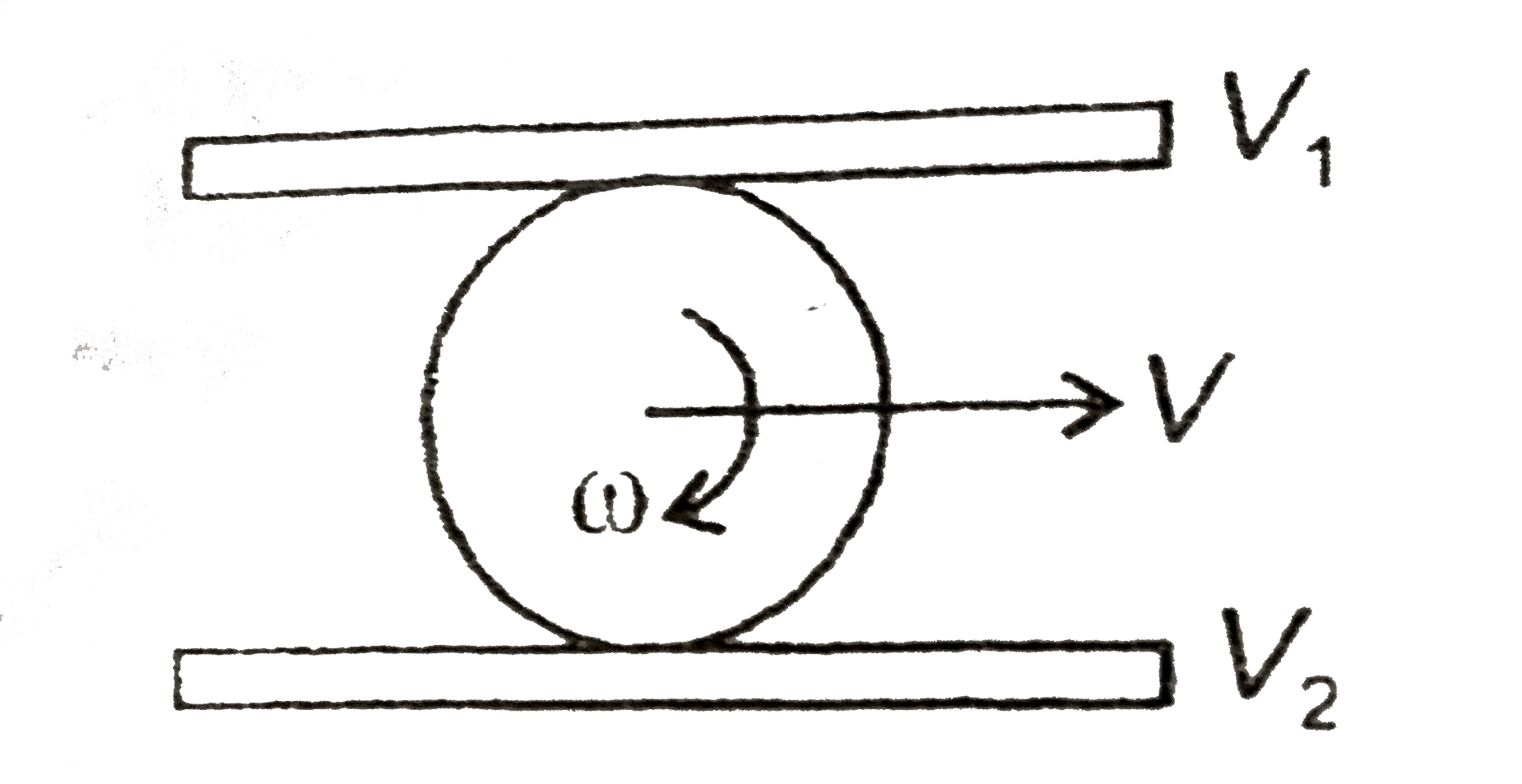
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find (a) Speed of centre of sphere (b) Angular velocity of the sphere
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R . Angular velocity and angular acceleration of line OA is omega and alpha respectively. Find the acceleration of point P on sphere.
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R . Angular velocity and angular acceleration of line OA is omega and alpha respectively. Find the acceleration of point P on sphere.
View Solution