A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
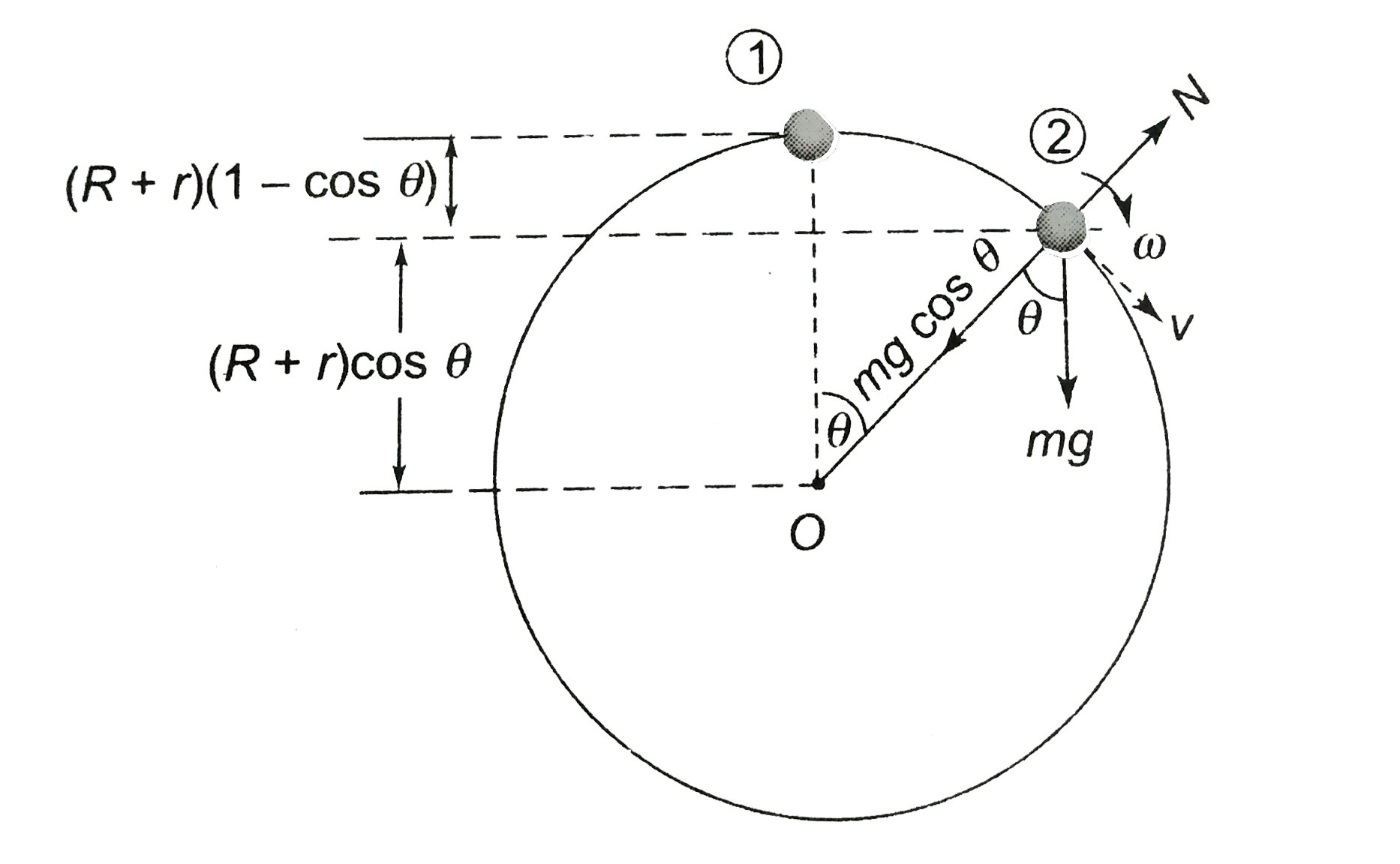
By the energy conservation between (1) and (2)
mg(R+r)(1−cosθ)=12mv2(1+25)
=710mv2 (i)
mgcosθ−N=mv2R+r (ii)
When the ball loses contact, we get
N=0 (iii)
From (i), (ii) and (iii), we have
mv2=mg(R+r)cosθ=107mg(R+r)(1−cosθ)
cosθ=107−107cosθ⇒cosθ=107
v=√g(R+r)cosθ=√10g(R+r)17
ω=vr=√10g(R+r)17r2
Recall: When a block is released from the top of a smooth hemisphere, it leaves contact at cosθ=2/3. Here the difference is due to the rotational motion.
Topper's Solved these Questions
Similar Questions
A uniform sphere of radius R16 starts rolling down without slipping from the top of another sphere of radius R=1m. The angular velocity of the sphere of in rads−1, after it leaves the surface of the larger sphere is 8xn. Where n=--
View SolutionA small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (figure) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.

View Solution
Knowledge Check
A uniform ball of radius R rolls without slipping between the rails such that the horizontal distance is √3R between the two contact points of te rails of the ball. Figure (a) shows front view of the ball and figure (b) shows the side view of the ball. vCM is the velocity of centre of mass of the ball and ω is the angular velocity of the ball after rolling down a distance 2h along the incline then
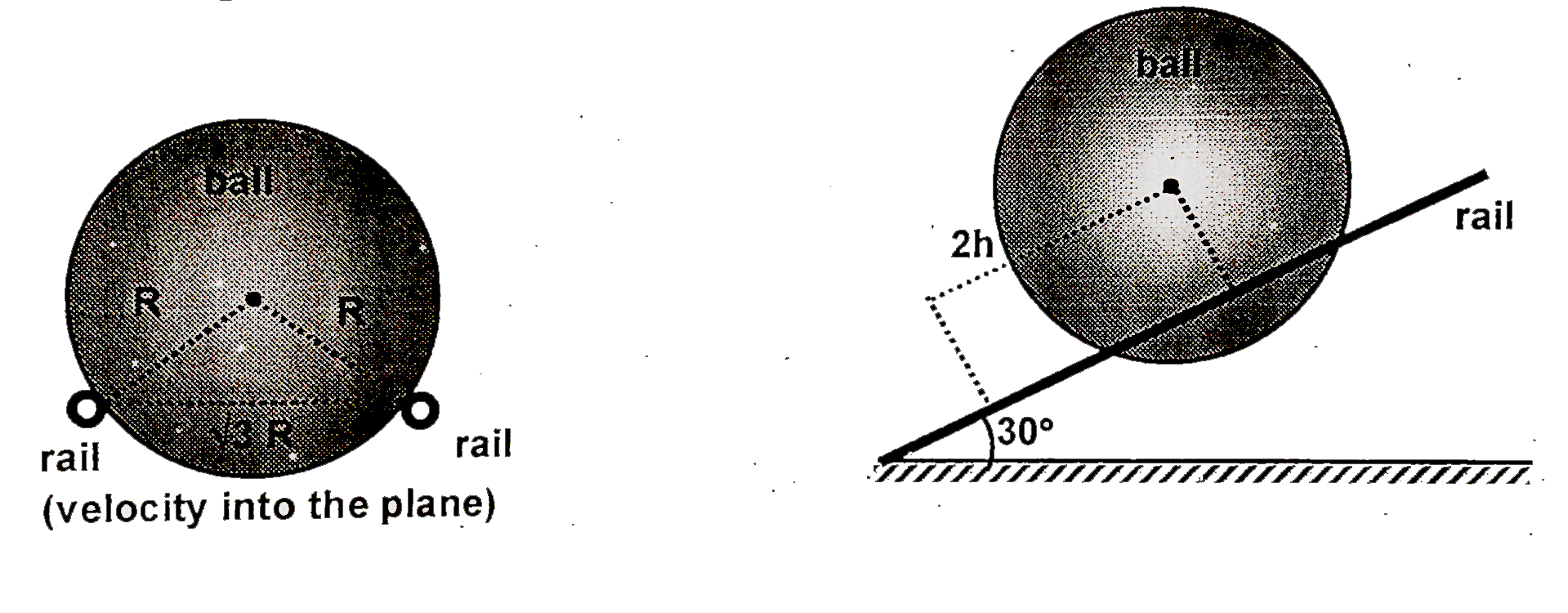 AVCM=ωRBVCM=ωR2CVCM=√10gh13DVCM=√10gh7
AVCM=ωRBVCM=ωR2CVCM=√10gh13DVCM=√10gh7A small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
A52RB52(R−r)C2510(R−r)D2710R−17r10A solid sphere of radius 'r' is rolling with velocity V on a smooth plane. The total kinetic energy of sphere is
A710mv2B34mv2C12mv2D14mv2
A uniform ball of radius r is placed on the top of a sphere of radius R = 10 r. It is given a slight push due to which it starts rolling down the sphere without slipping. The spin angular velocity of the ball when it breaks off from the sphere is ω=√pq(gr), where g is the acceleration due to gravity and p and q are the smallest integers. What is the value of p+q?
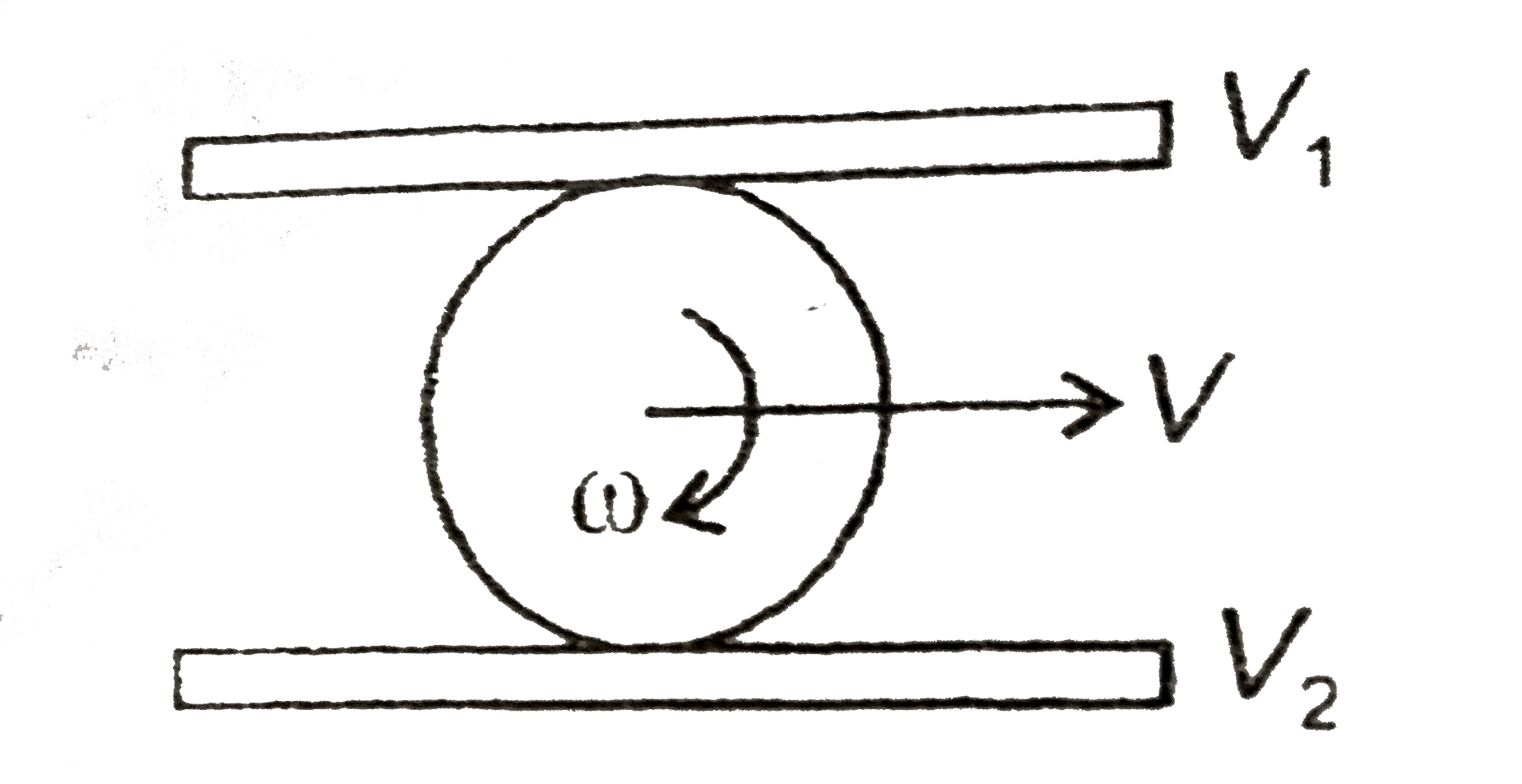
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA uniform sphere of mass m and radius R starts rolling without slipping down an inclined plane at an angle α to the horizontal. Find the time dependence of the angular momentum of the sphere relative to the point of contact at the initial moment. How will the obtained result change in the case of a perfectly smooth inclined plane?
View Solution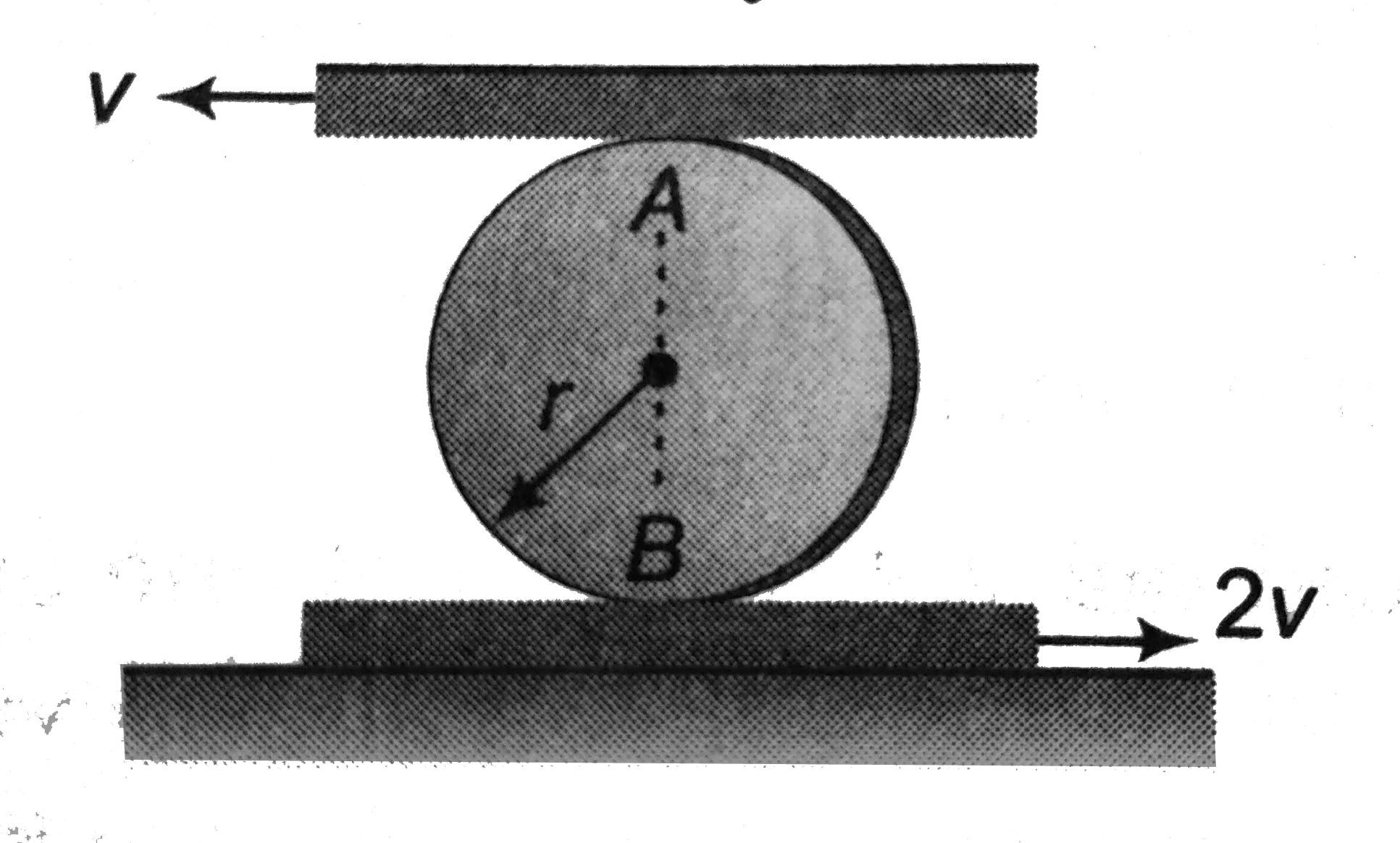
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View Solution
