A uniform ball of radius r is placed on the top of a sphere of radius R = 10 r. It is given a slight push due to which it starts rolling down the sphere without slipping. The spin angular velocity of the ball when it breaks off from the sphere is ω=√pq(gr), where g is the acceleration due to gravity and p and q are the smallest integers. What is the value of p+q?
The correct Answer is:127
To solve the problem, we need to find the spin angular velocity of a uniform ball when it breaks off from the surface of a larger sphere. Here's a step-by-step solution:
Step 1: Understand the Setup
We have a uniform ball of radius r placed on top of a sphere of radius R=10r. The ball rolls down the sphere without slipping.
Step 2: Determine the Height
When the ball is at the top of the sphere, its height from the reference point (the bottom of the sphere) is h=R+r=10r+r=11r.
Step 3: Apply Conservation of Energy
The total mechanical energy at the top (potential energy only) is equal to the total mechanical energy at the point just before it breaks off (potential energy + kinetic energy).
- At the top:
PEtop=mg(11r)
(where m is the mass of the ball and g is the acceleration due to gravity)
- At the point of breaking off:
- The height at this point is h=11rcosθ.
- The potential energy at this point:
PE=mg(11rcosθ)
- The kinetic energy consists of translational and rotational components:
KE=12mv2+12Iω2
where I=25mr2 (moment of inertia of a solid sphere) and ω=vr.
Step 4: Set Up the Energy Conservation Equation
Setting the total energy at the top equal to the total energy at the point of breaking off:
mg(11r)=mg(11rcosθ)+12mv2+12(25mr2)(v2r2)
Step 5: Simplify the Equation
Cancelling m from all terms and simplifying:
g(11r)=g(11rcosθ)+12v2+15v2
g(11r)=g(11rcosθ)+710v2
Step 6: Rearranging the Equation
Rearranging gives:
g(11r)(1−cosθ)=710v2
Step 7: Analyze Forces at the Point of Breaking Off
At the point of breaking off, the centripetal force is provided by the component of gravitational force:
mgcosθ=mv2R
Substituting R=11r:
gcosθ=v211r
Thus,
v2=11rgcosθ
Step 8: Substitute v2 Back into Energy Equation
Substituting v2 into the energy equation:
g(11r)(1−cosθ)=710(11rgcosθ)
Cancelling g and r:
11(1−cosθ)=710⋅11cosθ
1−cosθ=710cosθ
1=1710cosθ
cosθ=1017
Step 9: Find Angular Velocity ω
Now substituting cosθ back into the expression for v2:
v2=11rgcosθ=11rg⋅1017
Thus,
v2=110rg17
Using v=rω:
(rω)2=110rg17
ω2=110g17r
Taking the square root:
ω=√110g17r
Step 10: Identify p and q
Comparing with the given form ω=√pqgr:
- p=110
- q=17
Final Answer
Thus, p+q=110+17=127.
We have a uniform ball of radius r placed on top of a sphere of radius R=10r. The ball rolls down the sphere without slipping.
When the ball is at the top of the sphere, its height from the reference point (the bottom of the sphere) is h=R+r=10r+r=11r.
The total mechanical energy at the top (potential energy only) is equal to the total mechanical energy at the point just before it breaks off (potential energy + kinetic energy).
PEtop=mg(11r)
(where m is the mass of the ball and g is the acceleration due to gravity)
- The height at this point is h=11rcosθ.
- The potential energy at this point:
PE=mg(11rcosθ)
- The kinetic energy consists of translational and rotational components:
KE=12mv2+12Iω2
where I=25mr2 (moment of inertia of a solid sphere) and ω=vr.
Setting the total energy at the top equal to the total energy at the point of breaking off:
mg(11r)=mg(11rcosθ)+12mv2+12(25mr2)(v2r2)
Cancelling m from all terms and simplifying:
g(11r)=g(11rcosθ)+12v2+15v2
g(11r)=g(11rcosθ)+710v2
Rearranging gives:
g(11r)(1−cosθ)=710v2
At the point of breaking off, the centripetal force is provided by the component of gravitational force:
mgcosθ=mv2R
Substituting R=11r:
gcosθ=v211r
Thus,
v2=11rgcosθ
Substituting v2 into the energy equation:
g(11r)(1−cosθ)=710(11rgcosθ)
Cancelling g and r:
11(1−cosθ)=710⋅11cosθ
1−cosθ=710cosθ
1=1710cosθ
cosθ=1017
Now substituting cosθ back into the expression for v2:
v2=11rgcosθ=11rg⋅1017
Thus,
v2=110rg17
(rω)2=110rg17
ω2=110g17r
Taking the square root:
ω=√110g17r
Comparing with the given form ω=√pqgr:
- p=110
- q=17
Thus, p+q=110+17=127.
Topper's Solved these Questions
Similar Questions
A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionIf Q charge is given to a sphere of radius R, the energy of the system is
View Solution
Knowledge Check
A block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
AR4BR3CR2DRThe height at which the acceleration due to gravity becomes g9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth is
A2 RBR√3CR2D√2RThe height at which the acceleration due to gravity becomes g9 (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
AR√2BR /2C√2RD2R
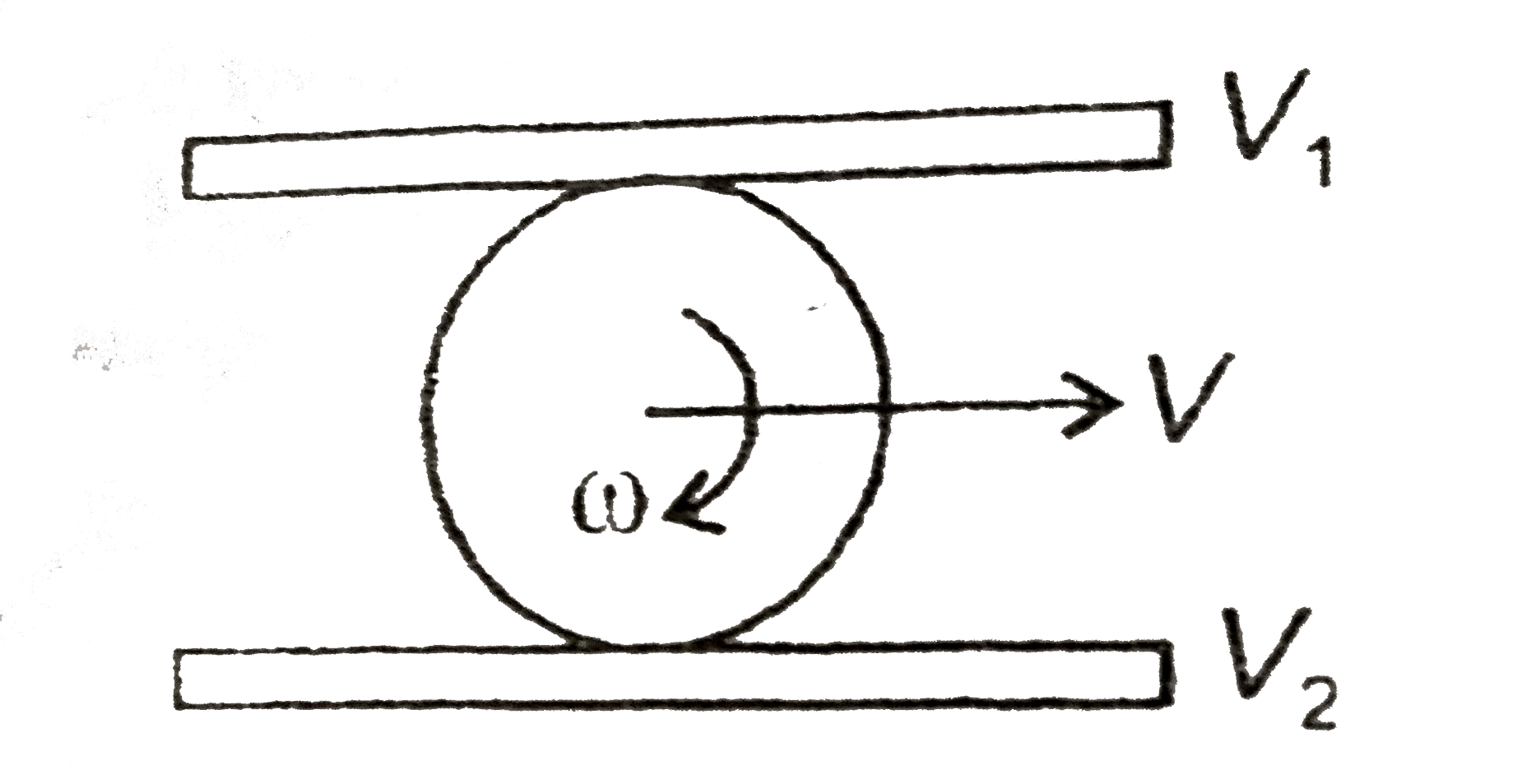
A sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (figure) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.

View SolutionA uniform sphere of mass m and radius R is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when h=7R/5.
View SolutionA uniform solid sphere of radius r=R5 is placed on the inside surface of a hemisherical bowl with radius R(=5r). The sphere is released from rest at an angle θ=37∘ to the vertical and rolls without slipping (Fig.) The angular speed of the sphere when it reaches the bottom of the bowl is.
 .
.
View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View Solution
