A rectangular tank filled with some liquid is accelerated along a horizontal surface at 403ms−2. Inside the liquid, a laser pointer is fixed a the centre of the tank which shoots a thin laser beam in the vertically upward direction. If after refraction from the liquid surface, the laser beam moves along the surface of the liquid, then what is the refractive index of the liquid ?
The correct Answer is:1.25
To solve the problem, we need to determine the refractive index of the liquid in the tank based on the given conditions. Here are the steps to arrive at the solution:
Step 1: Understand the Forces Acting on the Liquid
When the tank is accelerated horizontally, a pseudo force acts on the liquid in the opposite direction of the acceleration. The gravitational force acts downwards. The effective force acting on the liquid can be represented as a combination of these two forces.
Step 2: Determine the Angle of the Liquid Surface
The angle θ of the liquid surface can be found using the relationship between the gravitational force (g) and the pseudo force (a). The pseudo force is equal to the acceleration of the tank, which is given as 403m/s2.
Using the tangent of the angle:
tanθ=pseudo forcegravitational force=ag
Substituting the values:
tanθ=40310=43
Step 3: Calculate the Angle θ
From the tangent value, we can find θ:
θ=tan−1(43)
Step 4: Apply Snell's Law
When the laser beam passes from the liquid to the air, Snell's law applies:
n1sini=n2sinr
Where:
- n1 is the refractive index of the liquid (to be determined),
- n2=1 (the refractive index of air),
- i is the angle of incidence (which is equal to θ),
- r is the angle of refraction (which is 90° since the beam moves along the surface of the liquid).
Since sin90°=1, we can rewrite Snell's law as:
n1sinθ=1
Step 5: Calculate the Sine of θ
From the triangle formed by the forces, we can find sinθ:
sinθ=oppositehypotenuse=4√42+32=45
Step 6: Substitute into Snell's Law
Substituting sinθ into Snell's law:
n1⋅45=1
Thus,
n1=54
Step 7: Final Answer
The refractive index of the liquid is:
n1=1.25
Summary
The refractive index of the liquid in the tank is 1.25.
---
When the tank is accelerated horizontally, a pseudo force acts on the liquid in the opposite direction of the acceleration. The gravitational force acts downwards. The effective force acting on the liquid can be represented as a combination of these two forces.
The angle θ of the liquid surface can be found using the relationship between the gravitational force (g) and the pseudo force (a). The pseudo force is equal to the acceleration of the tank, which is given as 403m/s2.
tanθ=pseudo forcegravitational force=ag
Substituting the values:
tanθ=40310=43
From the tangent value, we can find θ:
θ=tan−1(43)
When the laser beam passes from the liquid to the air, Snell's law applies:
n1sini=n2sinr
Where:
- n1 is the refractive index of the liquid (to be determined),
- n2=1 (the refractive index of air),
- i is the angle of incidence (which is equal to θ),
- r is the angle of refraction (which is 90° since the beam moves along the surface of the liquid).
n1sinθ=1
From the triangle formed by the forces, we can find sinθ:
sinθ=oppositehypotenuse=4√42+32=45
Substituting sinθ into Snell's law:
n1⋅45=1
Thus,
n1=54
The refractive index of the liquid is:
n1=1.25
The refractive index of the liquid in the tank is 1.25.
Topper's Solved these Questions
Similar Questions
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?
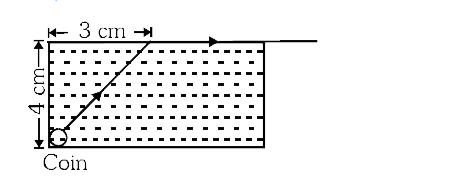
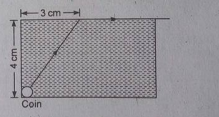
View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)
How fast is the light travelling in the liquid ?
View Solution
Knowledge Check
When the rectangular metal tank is filled to the top with an unknown liquid, as observer with eyes level with the top of the tank can just see the corner E, a ray that refracts towards the observer at the top surface of the liquid is shown. The refractive index of the liquid will be
 A1.2B1.4C1.6D1.9
A1.2B1.4C1.6D1.9When the rectangular metal tank is filled to the top with an unknown liquid, as observer with eyes level with the top of the tank can just see the corner E , a ray that refracts towards the observer at the top surface of the liquid is shown. The refractive index of the liquid will be
 A1.2B1.4C1.6D1.9
A1.2B1.4C1.6D1.9A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)

How fast is the light travelling in the liquid ?A1.8×108m/sB2.4×108m/sC3.0×108m/sD1.2×108m/s
A small coin is resting on the bottom of a beaker filled with liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface. How fast is the light travelling in the liquid?

View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?

View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure ).
How fast is the light travelling in the liquid ?

View SolutionA bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is h1 and that of the bird as estimated by the fish is h2, then the refractive index of the liquid is
View SolutionA tank, filled partially with a liquid, is subjected to a uniform horizontal acceleration. Which of the following is true for the surface of liquid in the tank?
View Solution

