A uniform ring of mass m radius r is suspended as shown in the figure. There are two horizontal axes A-A in the plane of ring and B-B perpendicular to the plane of ringAssertion A : Time period of small oscillations of ring about A-A and B - B is same.Reason R : T = √1/mgr where I is moment of inertia of ring.So time period is same for both cases.A A is correct & R is correct explanation of A.B Both are correct. But R is not correct explanation of A.C A is incorrect & R is correct.D Both are incorrect.
D Both are incorrect.Explanation:Hence both A & R are wrong.
Related Solutions
Find the out the moment of inertia of a ring having uniform mass distribution of mass and radius about an axis which is tangent ot the ring and in the plane of the ring . perpendicular to the plane of the ring.
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b . perpendicular to the plane of the ring.
View SolutionA uniform ring of radius 'R' is suspended from a horizontal nail 'A' as shown. Find time period of its small oscillations.
View SolutionA ring of radius R and mass M is pivoted at the rim and is set for small oscillation about an axis perpendicular to plane of ring. If a simple pendulum has to have the same time period as that of ring, the length of the pendulum should be
View SolutionA uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring is
View SolutionThe moment of inertia of a uniform circular ring, having a mass M and a radius R, about an axis tangential to the ring and perpendicular to its plane, is
View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View SolutionTwo rings of equal radius (r) and mass (m) are placed such that their centers are at a common point and their planes are perpendicular to each other. The moment of inertia of a system passing through the center of a ring and about an axis perpendicular to the plane of the ring is:
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2pisqrt((n(R-r))/(3g)) then find the value of n.
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2pisqrt((n(R-r))/(3g)) then find the value of n.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionM is mass and R is radius of a circular ring. The moment of inertia of same ring about an axis in the plane of ring at a perpendicular distance 2R/3 from centre of ring is
View SolutionCalculate the moment of inertia of a ring having mass , radius and having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
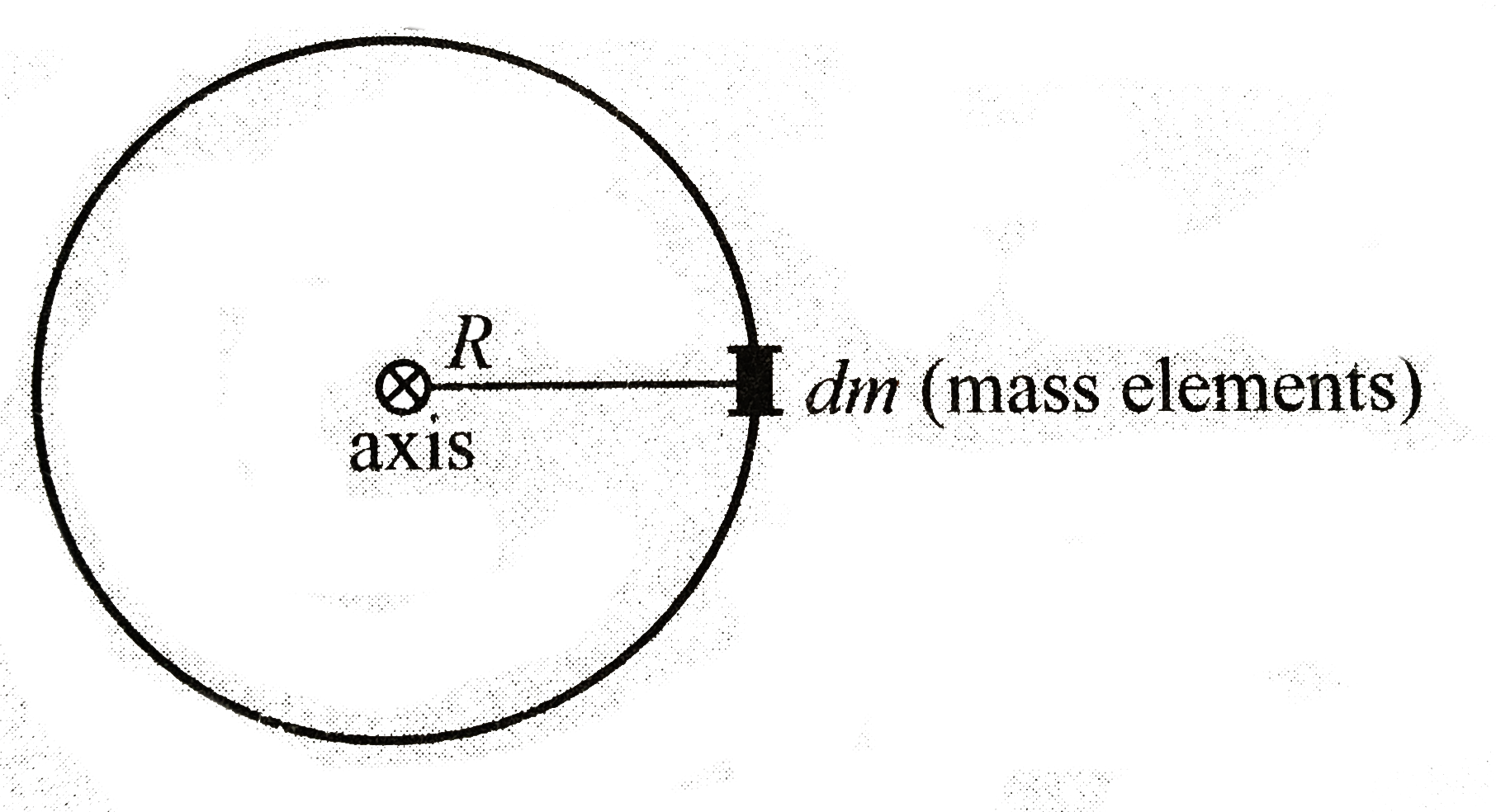
View SolutionCalculate the moment of inertia of a ring having mass M , radius R and having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
View SolutionA circular ring of radius r is placed in a homogeneous magnetic field perendicular to the plane of the ring. The field B changes with time according to the equation B=kt where K is constant and r is the time. The electric field in the ring is:
View SolutionMoment of inertia of a uniform circular ring of mass and radius about a diameter of ring is………………. .
View SolutionThe mass of a circular ring is and its radius is . Its moment of inertia about an axis in the plane of ring at perpendicular distance from centre of ring is
View Solutionएक r त्रिज्या की वृत्तीय वलय तल के लम्बवत् एकसमान चुम्बकीय क्षेत्र में स्थित है। चुम्बकीय क्षेत्र समय के साथ समीकरण के अनुसार परिवर्तित होता है, जहाँ k = स्थिरांक व t समय है। वलय में विद्युत क्षेत्र है
View SolutionCalculate the moment of inertia of a. a ring of mass M and radius R about an axis coinciding with the diameter of the ring. b. as thin disc about an axis coinciding with the diameter.
View Solution