Calculate the moment of inertia of
a. a ring of mass $M$ and radius $R$ about an axis coinciding with the diameter of the ring.
b. as thin disc about an axis coinciding with the diameter.

Video Solution

Text Solution

Verified by Experts

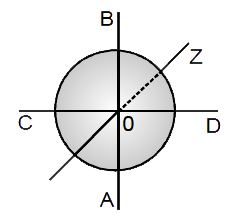
Let $X$ and $Y$ axis be along two perpendicular diameters of the ring.
BY symmetry $I_{x} = I_{y}$ and by perpendicular axis theorem $I_{z} = I_{x} + I_{y}$ .
But we know that $I_{z} = M R^{2}$
$M R^{2} = I_{x} + I_{y}^{z} = 2 I_{x}$
$\Rightarrow I_{x} = I_{y} = \frac{M R^{2}}{2}$
Situation of a thin disc (i.e. a circular plate) the moment of inertia about a diameter is
$I = \frac{1}{2} (\frac{1}{2} M R^{2}) = \frac{1}{4} M R^{2}$

Updated on:21/07/2023

Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
A $\frac{M R^{2}}{2}$
B $\frac{M R^{2}}{4}$
C $\frac{M R^{2}}{3}$
D $\frac{M R^{2}}{12}$
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $\frac{5}{2} M R^{2}$
B $\frac{3}{2} M R^{2}$
C $\frac{1}{2} M R^{2}$
D $M R^{2}$
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $M R^{2}$
B $\frac{1}{2} M R^{2}$
C $\frac{3}{2} M R^{2}$
D $\frac{7}{2} M R^{2}$