A thin rod of length L and area of crosssection S is pivoted at its lowest point P inside a stationary homogeneous & non-viscous liquid Figure. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. the density d1 of the material of the rod is smaller than the entity d2 of the liquid. The rod is displaced by a small angle θ from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
Torque on rod =
Related Solutions
A thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density of the rod is smaller than the density of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
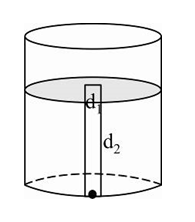
View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density of the rod is smaller than the density of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .

View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density of the rod is smaller than the density of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .

View SolutionLength L and Density d_(1) A thin cylindrical rod PQ is riveted at its lowest point P, which is a constant homogeneous and d_(2) The opacity occurs inside the liquid. The rod is always completely immersed inside the liquid and is about a horizontal axis passing through P. is free to rotate in the vertical plane. If d_(1)ltd_(2) What will be the time period of small angular oscillations with respect to the vertical equilibrium position of the rod?
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
View SolutionA rod of uniform mass and of length L can freely rotate in a vertical plane about an axis passing through O. The angular velocity of the rod when it falls from position P to P'' through an angle alpha is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle theta with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA thin uniform rod of length L and radius r rotates with an angular velocity in a horizontal plane about a vertical axis passing through one of its ends. The density of the material is and Youngs modulus is Y. 1) Find tension in the rod at distance Y from the axis. 2) Find elongation of the rod
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod is released from rest in the Position shown by slightly displacing it clockwise. Find the hinge reaction at the axis of rotation at the instant the rod turns through. 90^@
View SolutionA rod of length l is held vertically stationary with its lower end located at a point 'P', on the horizontal plane. When the rod is released to topple about 'P', the velocity of the upper end of the rod with which it hits the ground is
View SolutionA rod PQ of mass m and length L is rotated about an axis through P as shown in figure. Find the moment of inertia of the rod about the axis of rotation.

View SolutionA rod of length is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the of the rod when the rod is inclined at an angle from the vertical.

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle theta from the vertical.
View SolutionA homogenous rod XY of length L and mass 'M' is pivoted at the centre 'C' such that it can rotate freely in vertical plane. Initially the rod is in the horizontal position.
View SolutionA uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B . The rod begins rotating from rest. The angular velocity omega at angle theta is given as
View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.
View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.
View Solution