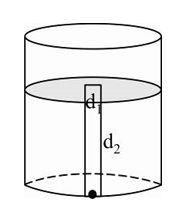
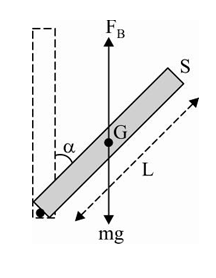
A thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
The correct Answer is:ω=√3g2L(d2−d1d1)
(ω=√3g2L(d2−d1d1))If the rod is displaced through an angle from its equilibrium position, i.e., vertical position then it will be under the thrust FB and its own weight mg. There will be a net torque, which will try to restore the rod to its equilibrium position.
Weight of the rod acting downward mg=SLd1g Buoyant force acting upwards =SLd2g
Net restoring torque τ=SL(d2−d1)gL2sinα
τ=SL(d2−d1)gL2sinα (because sinα=α)
If α is in clockwise direction, then τ will be in anticlockwise direction. Thus
τ=−12SL2(d2−d1)gα, τ=Iα=(ML23)d2adt2=(SLd1L23)d2adt2
therefore d2αdt2=3SL3d1(−12SL2(d2−d1)gα) or d2αdt2=−3g2L(d2−d1d1)
The angular frequency ω=√3g2L(d2−d1d1)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:6-previous year question
Explore 56 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
Similar Questions

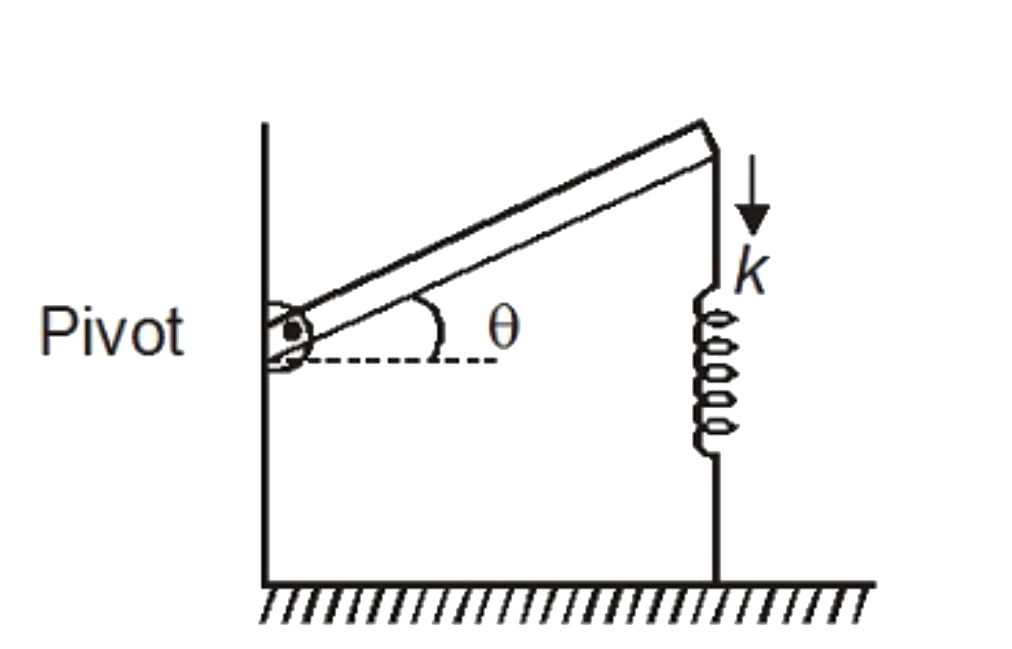
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA light rigid rod of mass M, and length L is pivoted at one of its end. The rod can swing freely in the vertical plane through a horizontal axis passing through the pivot. Show that the time period of the rod about the pivot is T=π√2L3g
View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View Solution

