A sphere of uniform density ρ has within it a spherical cavity whose centre is at a distance a from the centre of the sphere. The gravitational field within the cavity is :A non-uniform and zero at the center of the cavityB zero at every point inside the cavityC uniform and not zeroD same magnitude but has different direction at different points
Correct option: C uniform and not zeroExplanation:Gravitational field at P
Related Solutions
Inside a uniform sphere of density d there is a spherical cavity whose centre is at a distance r from the centre of sphere. The intensity of gravitational field inside the cavity is …
View SolutionInside a uniform sphere of density there is a spherical cavity whose centre is at a distance from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View SolutionInside a uniform sphere of density there is a spherical cavity whose centre is at a distance from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View SolutionA sphere of radius R has a uniform volume charge density . A spherical cavity of radius 'b' whose centre lies at is removed from the sphere. The electric field at any point of the spherical cavity is
View SolutionA non conducting sphere of radius a is charged uniform with volume charge density rho . There is a spherical cavity in the sphere with radius b. The position vector of centre of the cavity with respect to centre of the original sphere is vecC . Find the electric field at any point inside the cavity whose position vector is vecr with respect to centre of the original sphere.
View SolutionThe figure represents a solid uniform sphere of mass and radius . A spherical cavity of radius is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionThe figure represents a solid uniform sphere of mass and radius . A spherical cavity of radius is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionA uniform solid of valume mass density and radius R is shown in figure.
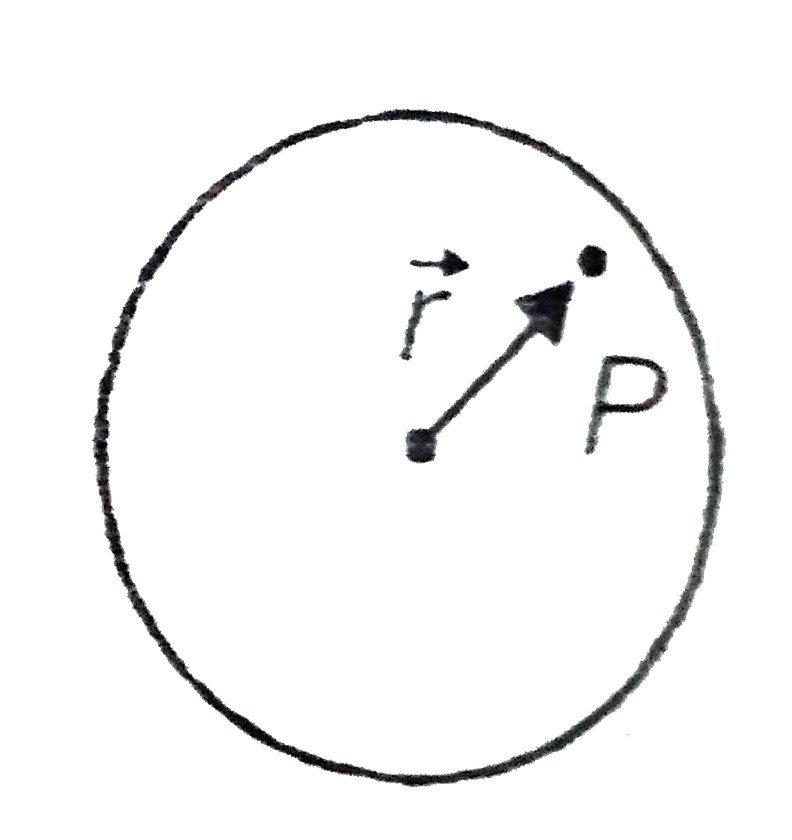
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector in terms of radius vector of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field at point P in vector formulationand interpret the result.
View SolutionA spherical cavity is made inside a sphere of density, d . Its centre lies at a distance l , from the centre of sphere, show that the gravitational strength, I , of the field inside the cavity is = (4//3) xx pi Gld .
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionThere is a uniformly charged non-conducting solid sphere. A small spherical cavity is made inside it. Distance of the centre of cavity is x from the centre of sphere
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA sphere of radius R has a uniform volume density . A spherical cavity of radius b, whose center lies at , is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.

View SolutionA sphere of radius R has a uniform volume density rho . A spherical cavity of radius b, whose center lies at veca , is removed from the sphere. i. Find the electric field at any point inside the spherical cavity. ii. Find the electric field outside the cavity (a) at points inside the large sphere but outside the cavity and (b) at points outside the large sphere.
View SolutionA fixed sphere of radius R and uniform density rho has a spherical cavity of radius R//2 such that the surface of the cavity passes through the centre of the sphere. A particle of mass m is located at the centre (A) of the velocity. Calculated (a) The gravitational field at A . (b) The velocity with which the particle strikes the centre O of the sphere. (Neglect earth's gravity)
View SolutionA : The gravitational field intensity is zero everywhere inside a uniform spherical shell
R: The net force on a point mass inside a uniform spherical shell is zero everywhere .
View SolutionA : The gravitational field intensity is zero everywhere inside a uniform spherical shell R: The net force on a point mass inside a uniform spherical shell is zero everywhere .
View SolutionA solid sphere of uniform density and mass M has radius 4m its centre is at the origin of the coordinate system two spheres of radii 1m are taken out so that their centres are at P(0,-2,0) and Q(0,2,0) respectively this leaves two spherical cavities what is the gravitational field at the centre of the cavities
View Solution