Complete Solutions to SOLVED EXAMPLES of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| MODERN PUBLICATION | SOLVED EXAMPLES |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
PQRS is a parallelogram and `oversetrarr(QS)` and `oversetrarr(PR)` are its diagonals .Show that
`vec(PR)+ vec(QS)-2vec(QR)=0`
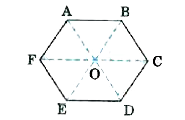
View SolutionFor a regular hexagon ABCDEF shown below , prove that
`overset rarr(AB)+ overset rarr(AC) +overset rarr(AD) +oversetrarr(AE)+oversetrarr(AF) = 6oversetrarr(AO).`
View SolutionA car travels 8 m due north and then 10 m due east Calculate the displacement of the car .
View SolutionTwo simultaneous forces are applied on a body , one 5N due east and other 7N due north . Find the result force on the body .
View SolutionA man walks 5 m toward west and 12 m toward north and then 7 m vertically upward . Calculate the magnitude of sum of these displacements .
View SolutionTwo forces of 12 N and 5 N are acting on a particle , with an angle of `60^(@)` between them , Calculate the resultant force .
View SolutionProve that the resultant of two vector of equal magnitude is equal to either vector if the angle between the two vector is `120^(@)`
View SolutionThe magnitudes of two forces X and Y are in the ratio `2:3` . If the resultant of two forces is 25N and angle between them `60^(@)`, find the magnitude of each force close to one place of decimal .
View SolutionThe greatest and least resultant of two force acting on a particle are 16 N and 9N, respectively . If the first force is double and the second force is incresed by 5.5N, calculate the resultant of two new force, acting at right angle to each other .
View SolutionFour forces are acting on a particle simultaneously : 50N due east , 40 N due north , 30 N due west and 20 N due south . Calculate the resultant force on the particle .
View SolutionRain is falling vertically with a speed of `35 m s^(-1)` . A woman rides a bicycle with a speed of ` 12 m s^(-1)` in east to west direction. In which direction should she hold her umbrella ?
View SolutionA motor boat is racing towards North at `25 km//h` and the water current in that region is `10 km//h` in the direction of `60 ^(00` East of South. Find the resultant velocity of the boat.
View SolutionA swimmer wants to cross a 600 m wide river . If the speed of swimmer is 12 km/hr in still water and speed of river is 6km/hr , along what direction the swimmer must strike in order to cross the river straight ? Also, calculate his resultant velocity and time taken by him to do so .
View SolutionFor the vectors `vecA=hati+2 hat j-hatk and vecB=2 hati+3hatj+2hatk`,
find the vector `vec(AB)` and its magnitude.
View SolutionFor the vectors `vecA and vecB` in the above example , find unit vector parallel to the resultant of the two vectors
View SolutionWhen a vector `vecC` is added to the resultant of vectors
`vecA=hati+4hatj-2hatk and vecB=3hati-5hatj+hatk`, a unit vector along
Z-axis is obtained . Find the vector `vecC`
View SolutionCalculate the value of `beta` in the unit vector `0.8 hati-0.4hatj-betahatk` .
View SolutionFind a vector having same magnitude as vector `vecA=6hati+18hatj` and parallel to vector `vecB=2hati+5 hatj`.
View SolutionA velocity is inclined at `30^(@)` to the horizontal . If its rectangular component in horizontal direction is `40 km//hr` , find the magnitude of velocity and its vertical component.
View SolutionTwo billiard ball, rolling a flat table, have started moving from the same point. If their x components of velocities are `sqrt3m//s` and `2m//s` and y components of velocities are `1m//s` and `2m//s` , respectively, calculate the angle between their paths .
View SolutionCalculate the angle between the two vectors
`vecA=-2hati+hatj-3hatk and vecB =hati-2hatj+hatk`
View SolutionFor the two vectors `vecA=2hati-hatj` and `vecB=hati + alpha hatj+3hatk`, perpendicular to each other , find the value of a .
View SolutionIf the magnitude of two vectors are ` 3 ` and `6` and ther scalar product is `9`, find the angle between the two vectors.
View SolutionA body constrained to move along the Y-axis of a co-ordinate system is subjected to a constant force `vecF` given unit `vecF=-hati+6hatj+2 hatk` newton where `hati, hatj and hatk` represent unit vector along X-, Y- and Z-axis of the system , respectively . Calculate the work done by the force in displacement the body through a distance of 4 m along the Y-axis .
View SolutionIf the magnitude of there vectors `vec X, vecY and vecZ` are 4, 3 and 5, respectively and `vecX+vecY=vecZ`, then calculate the angle between `vecY and vecZ`.
View SolutionFor three vectors `vecP, vecQ and vecR, vecP+vecQ=vecR and P+Q=R`
Then prove that `vecP and vecQ` are parallel to each other.
View SolutionFind the vector product of two vectors `vecA=4 hati+3 hatj+hatk and hatB =3 hat i+2 hat j+4 hat k`.
View SolutionShown that the vectors `3 hati+3 hatj+9hatk and hati+hatj+3hatk` are parallel.
View SolutionFind a unit vector perpendicular to both vectors
`vecA=3hati+4hatj and vecB=-3hati+7hatj`.
View SolutionCalculate the area of a parallelogram whose adjacent sides are formed by the vectors `vecA=hati-3hatj+hatk` and `vecB=2hati-hatj+3hatk` .
View SolutionCalculate the sine of the angle between the vectors
`vecA=3hati-4hatj+5hatk and vecB=-2hati+hatj-2hatk` .
View SolutionFor two vectors `vecP and vecQ` , show that
`(vecP+vecQ)xx(vecP-vecQ)=2(vecQxxvecP)`
View SolutionIf `vecA=2hati-hatj-3hatk and vecB=hati+2hatj-hatk and vec C=hati+3hatj-2hatk` find `(vecAxxvecB)xxvecC`
View SolutionCalculate the area of the triangle formed by the tips of vectors `vecP=2hati+hatj-3hatk, vecQ=3hati-hatj+2hatk` and
`vecR=4hati-3hatj+hatk`
View SolutionDetermine the area of a parallelogram whose diagonals are given by vectors `3hati+2hatj-7hatk and 5hati+6hatj-3hatk` .
View SolutionCalculate the moment of force about the point `i-2hatj-hatk` of the force `3i-5hatj+hatk` acting at the point `-2hati-hatk.`
View SolutionAn athlete is running on a circular track of radius 1m with a uniform velocity of `20m//s` . Calculate
(i) the difference in the magnitude of the displacement of the athlete and the distance covered by him in completing half a ground .
(ii) magnitude of change in velocity of the athlete in half a round .
View SolutionThe position of a particle is given by `vecr =3.0t veci+2.0t^(2) hatj+5.0 hatk`
Where is in seconds and the coefficients have the proper unit for r to be in maters . (a) Find v(t) and a(t) of the particle .
(b) Find the magnitude and direction of `v(t) "at" t=1.0s`
View SolutionA cricket ball is thrown at a speed of ` 28 ms^(-1)` in a direction `30 ^(@)` above the horizontal. Calculate (a)the maximum height (b) the time taken by ball to return ti the same level, and (c )the distance from the thrower to the point wher the ball restance from the throwrt to the point where the ball returns to the same level.
View SolutionA boy stands 19.6 m away from a 9.8m high cliff. If the throws a ball towards the cliff such that it just passes above from it , find the velocity of projection of the ball.
View SolutionA projectile when fired at a certain inclination has maximum rang R. Find its maximum height attained by it in terms of R .
View SolutionA stone is projected at an angle of `30^(@)` with the vertical. If the horizontal component of its velocity is `9.8m//s` , calculate the maximum height attained by the stone and its horizontal range .
View SolutionTwo balls A and B are thrown from the same point with similar velocity of `19.6 m/s` , at angle `theta` and `90^(@)-theta` with the horizontal , respectively . Ball B reaches 10 m higher than ball A. Find the individual maximum higher reached by ball A and B .
View SolutionShow that the horizontal range of a projectile is same for two angles of projection . Is the sum of maximum heights for these two angles dependent on the angle of projectile ?
View SolutionTwo projectiles are projected from the same point different velocities and different angles of projection .If the maximum height attained by both the projectiles is same, show that sum of the times taken by each to reach the highest point is equal to the total time of flight of either of the projectiles .
View SolutionA person sees an object on a tree at a heitht of ` 40 m` and at a distance of ` 60 m` . Whith what velocity he showld throw an arrow at an angle of `45^@` so that it may hit the object ? Take ` g= 10 ms^(2)`.
View SolutionA stone is thrown from a cliff 4.2 m high . At what angle he must incline his rifle in order to cover a maximum range of firing on the ground below . Taken muzzle velocity of bullet `=20m//s` and `g=10ms^(-2)`.
View SolutionTwo bodies A and B are projected simultaneously from points X and Y as shown in the figure, with velocities `u_(A)` and `u_(B)` respectively.

Find the ratio of `(u_(A))/(u_(B))` for both the bodies to collide .
View SolutionA stone is thrown horizontally from the top of a cliff and strikes the ground after 5 seconds, at an angle of `45^(@)` with the horizontal . Calculate
(i) height of the cliff.
(ii) speed of projection of the stone .
View SolutionA hiker stands on the edge of a cliff `490 m` above the ground and throwns a stone horiozontally with an initial speed of `15ms^(-1)` neglecting air resistance.The time taken by the stone to reach the ground in seconds is `(g=9.8ms^(2))`
View SolutionA pocket is dropped from an aeroplane when it is directly above a point X on the ground and hits the ground at Y. If the aeroplane is moving horizontally with a speed of 600 km/h, 1, 000m above the ground , find the distance XY.
View Solutiontwo tall building are situated 300 m apart . A ball is thrown horizontally from the window of `10^(th)` floor of one building such that it lands in a windo of `3^(rd)` floor of another nuilding. If the vertical distance between the corresponding floors of the building is 5m, find the velocity with which the ball must be thrown .
View SolutionA particle is thrown horizontally from the top of an inclined plane , with a speed of `5 m//s` . If the inclination of the plane is `30^(@)` with the horizontal , how far from the point of projection will the particle strike the plane ?
View SolutionA helicopter moving horizontally with a velocity of 360 km/h has to drop a food packet directly into a relief fund office . If the height of helicopter from the ground is 200 m , at what distance the helicopter must be from the fund office when the packet is dropped ?
View SolutionWhat are the angular velocities of a second hand, minute hand and hour hand of a clock ?
View SolutionA body of mass 0.5 kg made to revolve in a horizontal circle of radius 3 m with a uniform speed of `12 mm/s` . Find its
(i) angular speed
(ii) frequency of revolution.
(iii) time period .
(iv) centripetal acceleration.
View SolutionAn insect trapped in a circular groove of radius `12 cm` moves along the groove steadily and commpletes ` 7` revoltions in `100 s.` (a) What is the angulr speed , and thelinear speed of the motion ? (b) Is the acceleration vector a costant vector ? What is its magnitude?
View SolutionThe earth revolves around the sun in an orbit of radius `15xx10^(10)` m .Find the angular and linear velocity of the earth . Also calculate the angle through which the earth revolves in a day .
View SolutionA particle is moving in a circle of radius 0.3 . Calculate its linear acceleration at the instant when its angular velocity is `1rad//s` and angular acceleration is `4rad//s^(2)`
View SolutionA car is moving with a velocity of `60km//h` due east and a train is moving with a velocity of `80km//h` due south . For a passenger sitting inside the train , what is the velocity of car appearing to him ?
View SolutionA body A is moving along a straight path with a velocity of `4m//s` Another body B is moving with a velocity of `5m//s`, on a traight path, at an angle of `45^(@)` to the path of A. Calculate the spend of B relative to A.
View SolutionA ship is sailing towards east in a traight line motion, with a speed of `10m//s` . A man on the deck is moving across it , towards north, with a speed of `6 m//s`
calculate the velocity of the man relative to the sea.
View SolutionA man rows across a flowing river in time `t_(1)` and rows an equal distance downstream in time `t_(2)`. Calculate the ratio `t_(1):t_(2)` if the speed of man in still water is `5 m//s` and speed of stream is `3m//s` .
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter MOTION IN A PLANE of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS MOTION IN A PLANE
- Chapter Practice Test
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (A. Multiple Choice Questions)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (Assertion Reason Type Questions)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (B. Multiple Choice Questions)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (C. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (JEE (Advanced) for IIT Entrance)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other Boards for Engineering Entrance)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS)
- COMPETITION FILE OBJECTIVE TYPE QUESTIONS (NCERT (Exemplar Problems Objective Questions))
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level
- NCERT FILE (Solved) (NCERT (Additional Exercises))
- NCERT FILE (Solved) NCERT (Textbook Exercises)
- NCERT FILE (Solved) (NCERT (Exemplar Problems Subjective Questions) Very short nswer type questions)
- PRACTICE PROBLEMS
- PRACTICE PROBLEMS (1)
- PRACTICE PROBLEMS (2)
- PRACTICE PROBLEMS (3)
- PRACTICE PROBLEMS (4)
- PRACTICE PROBLEMS (5)
- PRACTICE PROBLEMS (6)
- Revision Exercises (Additional Questions)
- Revision Exercises (Fill in the Blanks)
- Revision Exercises (Long Answer Question)
- Revision Exercises (Numerical Problems)
- Revision Exercises (Short Answer Question)
- Revision Exercises (very Short Answer Questions)
- SOLVED EXAMPLES
- TOUGH & TRICKY PROBLEMS