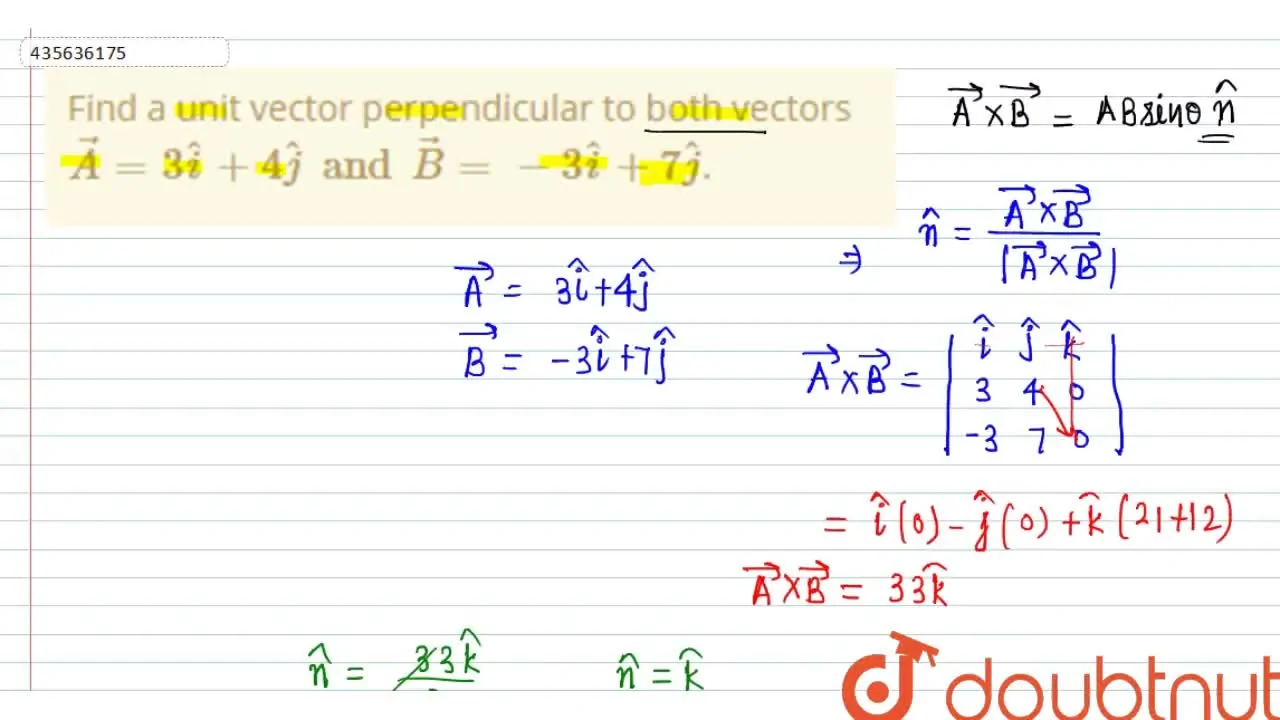
Find a unit vector perpendicular to both vectors
→A=3ˆi+4ˆjand→B=−3ˆi+7ˆj.
We know that
→A×→B=ABsinθˆn=∣∣→A×→B∣∣ˆn
where ˆn is the required unit vector, perpendicular to both →Aand→B .
∴ˆn=→A×→B∣∣→A×→B∣∣
Now , →A×→B=∣∣
∣
∣∣ˆiˆjˆk340−370∣∣
∣
∣∣
=(4×0−0×7)ˆi+(0×−3−0×3)ˆj+(3×7+3×4)ˆk
=0ˆi+0ˆj+33ˆk=33ˆk
∣∣→A×→B∣∣=√02+02+332=33
∴ˆn=33ˆk33=ˆk
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (1)8videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (2)9videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test16videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
Similar Questions
Determine a unit vector perpendicular to both the vectors →A=2ˆi−3ˆj+6ˆkand→B=ˆi−2ˆj+4ˆk
View SolutionFind a unit vectro perpendicular to the vectors →a=3ˆi+2ˆj−ˆkand→b=12ˆi+5ˆj−5ˆk Also determine the sine of the angle between →aand→b.
View SolutionFind the unit vector perpendicular to the vectors →A=(ˆi+2ˆj−3ˆk)and→B=(−ˆi+ˆj−ˆk)
View SolutionFind the unit vector perpendicular to ltbr> →A=3ˆi+2ˆj−ˆk and →B=ˆi−ˆj+ˆk
View SolutionFind a unit vector perpendicular to each of the vectors 2ˆi−3ˆj+ˆk and 3ˆi−4ˆj−ˆk.
View SolutionFind a unit vector perpendicular to both the vectors ˆi−2ˆj+ˆk and ˆi+2ˆj+ˆk.
View SolutionFind a unit vector perpendicular to both the vectors 2ˆi+3ˆj+ˆk)and(ˆi−ˆj+2ˆk).
View SolutionFind a unit vector perpendicular to each of the vectors ˆi+2ˆj−3ˆk and ˆi−2ˆj+ˆk.
View SolutionFind the unit vector perpendicular to each of the vectors →a=3ˆi+2ˆj−3ˆk and →b=ˆi+ˆj−ˆk.
View SolutionFind a unit vector perpendicular to each one of the vectors →a=4ˆi−ˆj+3ˆkand→b=3ˆi+2ˆj−ˆk
View Solution