A body A is moving along a straight path with a velocity of 4m/s Another body B is moving with a velocity of 5m/s, on a traight path, at an angle of 45∘ to the path of A. Calculate the spend of B relative to A.
To find the speed of body B relative to body A, we can follow these steps:
Step 1: Identify the velocities
- Velocity of body A, VA=4m/s (along the x-axis).
- Velocity of body B, VB=5m/s at an angle of 45∘ to the path of A.
Step 2: Resolve the velocity of B into components
Since body B is moving at an angle of 45∘, we can resolve its velocity into horizontal (x) and vertical (y) components:
- VBx=VBcos(45∘)=5⋅1√2=5√2m/s
- VBy=VBsin(45∘)=5⋅1√2=5√2m/s
Step 3: Write the relative velocity equation
The relative velocity of B with respect to A is given by:
VBA=VB−VA
Since A is moving along the x-axis, we can write:
VBAx=VBx−VA=5√2−4
VBAy=VBy=5√2
Step 4: Calculate the components
Now, we need to calculate VBAx:
VBAx=5√2−4
To simplify this, we can convert 4 into a fraction with a common denominator:
4=4√2√2
Thus,
VBAx=5−4√2√2
Step 5: Calculate the magnitude of the relative velocity
Now we can find the magnitude of the relative velocity VBA:
VBA=√(VBAx)2+(VBAy)2
Substituting the values:
VBA=
⎷(5−4√2√2)2+(5√2)2
Step 6: Simplify and calculate
Calculating each term:
1. (VBAx)2=(5−4√2√2)2
2. (VBAy)2=(5√2)2=252
Now, we can compute the final result:
VBA=
⎷((5−4√2)22)+252
Final Calculation
After calculating the above expression, we find that:
VBA≈3.5m/s
Final Answer
The speed of body B relative to body A is approximately 3.5m/s.
---
- Velocity of body A, VA=4m/s (along the x-axis).
- Velocity of body B, VB=5m/s at an angle of 45∘ to the path of A.
Since body B is moving at an angle of 45∘, we can resolve its velocity into horizontal (x) and vertical (y) components:
- VBx=VBcos(45∘)=5⋅1√2=5√2m/s
- VBy=VBsin(45∘)=5⋅1√2=5√2m/s
The relative velocity of B with respect to A is given by:
VBA=VB−VA
Since A is moving along the x-axis, we can write:
VBAx=VBx−VA=5√2−4
VBAy=VBy=5√2
Now, we need to calculate VBAx:
VBAx=5√2−4
To simplify this, we can convert 4 into a fraction with a common denominator:
4=4√2√2
Thus,
VBAx=5−4√2√2
Now we can find the magnitude of the relative velocity VBA:
VBA=√(VBAx)2+(VBAy)2
Substituting the values:
VBA=
⎷(5−4√2√2)2+(5√2)2
Calculating each term:
1. (VBAx)2=(5−4√2√2)2
2. (VBAy)2=(5√2)2=252
VBA=
⎷((5−4√2)22)+252
After calculating the above expression, we find that:
VBA≈3.5m/s
The speed of body B relative to body A is approximately 3.5m/s.
Topper's Solved these Questions
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:PRACTICE PROBLEMS (1)
Explore 8 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:PRACTICE PROBLEMS (2)
Explore 9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Chapter Practise Test
Explore 16 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
Similar Questions
A particle P is moving along a straight line with a velocity of 3ms−1 and another particle Q has a velocity of 4ms−1 at an angle of 30∘ to the path of P. Find the speed of Q relative to P.
View SolutionA body moving along a straight path covers one-third of a distance with a velocity of 5 Kmph and the rest of the path with a velocity of 20 Kmph. Find the average velocity of the body.

View Solution
Knowledge Check
A body moving along a circular path has
Aa constant speedBa constant velocityCno tangential velocityDno radial accelerationA body moving along a circular path has
Aa constant speedBa constant velocityCno tangential velocityDno radial acceleration.A body of mass 1kg is moving along a straight line with a velocity of 1m/s. The external force acting in the body is
A1NB1 dyneC1JDzero
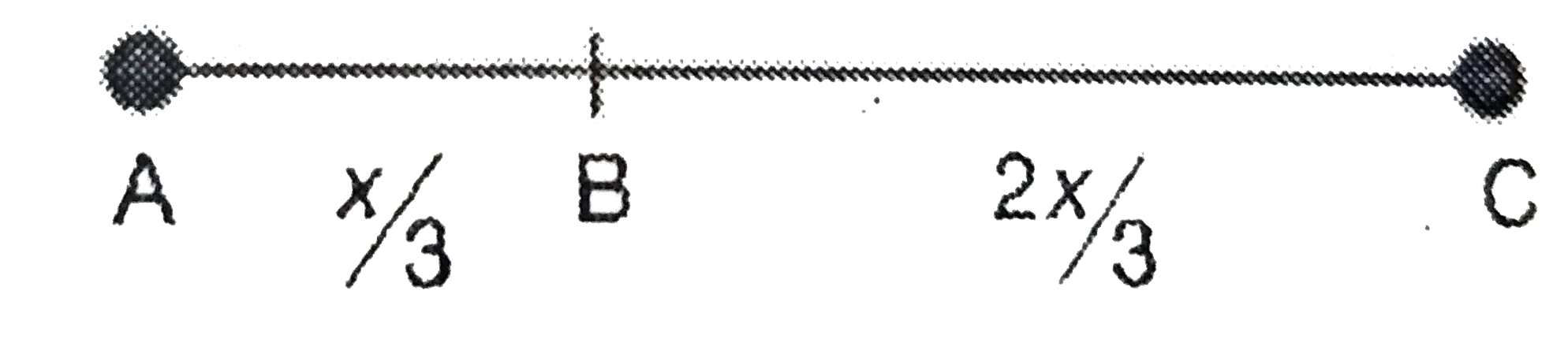
A body moving along a straight path covers one-third of a distace with a velocity of 5 Kmph and the rest of the path with a velocity of 20 Kmph.
Find the average velocity of the body
View Solution0A body of mass 20 kg moving with a velocity of 3 m/s, rebounds on a wall with same velocity. The impulse on the body is -
View SolutionIf a particle A is moving along a straight line with velocity 3m/s and another particle B has a velocity 5m/s at an angle of 60∘ to the path of A then the velocity B relative to A is
View SolutionIf a particle A is moving along a straight line with velocity 3m/s and another particle B has a velocity 5m/s at an angle of 60∘ to the path of A then the velocity B relative to A is
View SolutionA body is moving in a circular path with a constant speed. It has .
View Solution