A motor boat is racing towards North at $25 k m / h$ and the water current in that region is $10 k m / h$ in the direction of $60^{00}$ East of South. Find the resultant velocity of the boat.

Video Solution

Text Solution

Verified by Experts

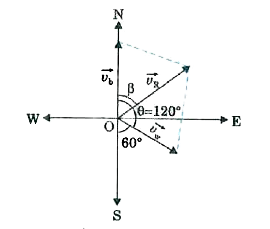
Let O be the origin of journey of the motor boat
Here, ${\to v}_{b}$ =velocity of motor boat
$= 25 k m / h r$ , due north
${\to v}_{w}$ =velocity of water current
$= 10 k m / h r, 60^{\circ}$ east of south
$θ = 120^{\circ}$
The magnitude of the resultant velocity $| {\to v}_{R} |$ is given by:
$| {\to v}_{R} | = \sqrt{v_{b}^{2} + v_{w}^{2} + 2 v_{b} + v_{w} {cos 120}^{\circ}}$
$= \sqrt{25^{2} + 10^{2} + 2 \times 25 \times 10 \times (\frac{- 1}{2})}$
$= 21.8 k m / h r$
Let ${\to v}_{R}$ make an nagle of $β$ with ${\to v}_{b}$ . Then
$tan β = \frac{v_{w} sin θ}{v_{b} + v_{w} cos θ} = \frac{10 \times {sin 120}^{\circ}}{25 + 10 {cos 120}^{\circ}}$
$= \frac{\frac{10 \times \sqrt{3}}{2}}{25 - 10 \times \frac{1}{2}} = \frac{\sqrt{3}}{4}$
$β = {tan}^{- 1} (\frac{\sqrt{3}}{4}) = {tan}^{- 1} (0.433) = {23.4}^{\circ}$

Updated on:21/07/2023

A boat is moving towards east velocity 4 m/s w.r.t still water and river is flowing towards north with velocity 2 m/s and the wind blowing towards north with velocity 6 m/s. the direction of the flag blown over by the wind hpisted on the boat is
ANorth - west
Bsouth- west
C ${tan}^{- 1} (\frac{1}{2})$ with east
DNorth
A car $A$ going north-east at $80 k m / h$ and another car $B$ is going south-east at $60 k m / h .$ The direction of the velocity of $A$ relative to $B$ makes an angle with the north equal to:
A ${tan}^{- 1} (2 / 7)$
B ${tan}^{- 1} (7 / 2)$
C ${tan}^{- 1} (7)$
D ${tan}^{- 1} (1 / 7)$
A boat is moving towards south with veloctity $3 m / s$ with respect to still water and river is flowing towards east with velocity $3 m / s$ and the wind is blowing towards south-east with velocoity $3 \sqrt{2} m / s$ . The direction of the flag blown over by the wind, hoisted on the boat is :
Anorth-west
Bsouth-east
Cthe flag will not blow
Dnorth