The velocity of a body is 100kmh−1, 30^(@) west of south . Find the north ad east components of the vector.
The angke which the given velocity makes with thenorth direction is 180∘−30∘=150∘. The component velocity aling north =vcos150∘.
=100×(−√3/2)=−86.6kmh−1
The angle which the given velocity makes with the east direction is 90∘+30∘. The component velocity along east =vcos120∘
=100×(−1/2)
=−50kmh−1.
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 Short answer
Explore 30 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:5 Short answer
Explore 6 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:2 Short answer
Explore 26 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
A motor boat is racing towards North at 25km/h and the water current in that region is 10km/h in the direction of 6000 East of South. Find the resultant velocity of the boat.
View SolutionA man rows a boat with a speed of 18Kmh−1 in the north-west direction (figure). The shoreline makes an angle of 15∘ south of west. Obtain the components of the velocity of the boat along the shoreline and perpendicular to the shoreline.

View Solution
Knowledge Check
One of the rectangular components of a velocity of 60 kmh−1 is 30 km h−1 . Find other rectangular component ?
A15√3kmh−1B30√6kmh−1C30√3kmh−1D15√6kmh−1A ship is travelling due east at 10 km/h. A ship heading 30∘ east of north is always due north from the first ship. The speed of the second ship in km/h is
A20√2B20√3/2C20D20/√2Ship A is travelling with a velocity of 5kmh−1 due east. A second ship is heading 30∘ east of north. What should be the speed of second ship if it is to remain always due north with respect to the first ship ?
A10kmh−1B9kmh−1C8kmh−1D7kmh−1
A motor boat is racing towards North at 25km/h and the water current in that region is 10km/h in the direction of 6000 East of South. Find the resultant velocity of the boat.
View SolutionA train is moving with a velocity of 30kmh−1 due East and a car is moving with a veloicty of 40kmh−1 due North . What is the velocity of car as appears to a passenger in the train ?
View SolutionRepresent the following graphically a displacement of :
(i) 40 km, 30∘ west of south
(ii) 40 km, 30∘ east of south
(iii) 40 km, 30∘ west of north.
View SolutionRepresent the following graphically:
(i) A displacement of 40km, 30∘ west of south,
(ii) a displacement of 70km, 40∘ north of west.
View SolutionA man walks towards east with certain velocity. A car is travelling along a road which is 30∘ west of north. While a bus is travelling in another road which is 60∘ south of west. Find the angle between velocity vector of
(a) man and car (b) car and bus
(c) bus and man.
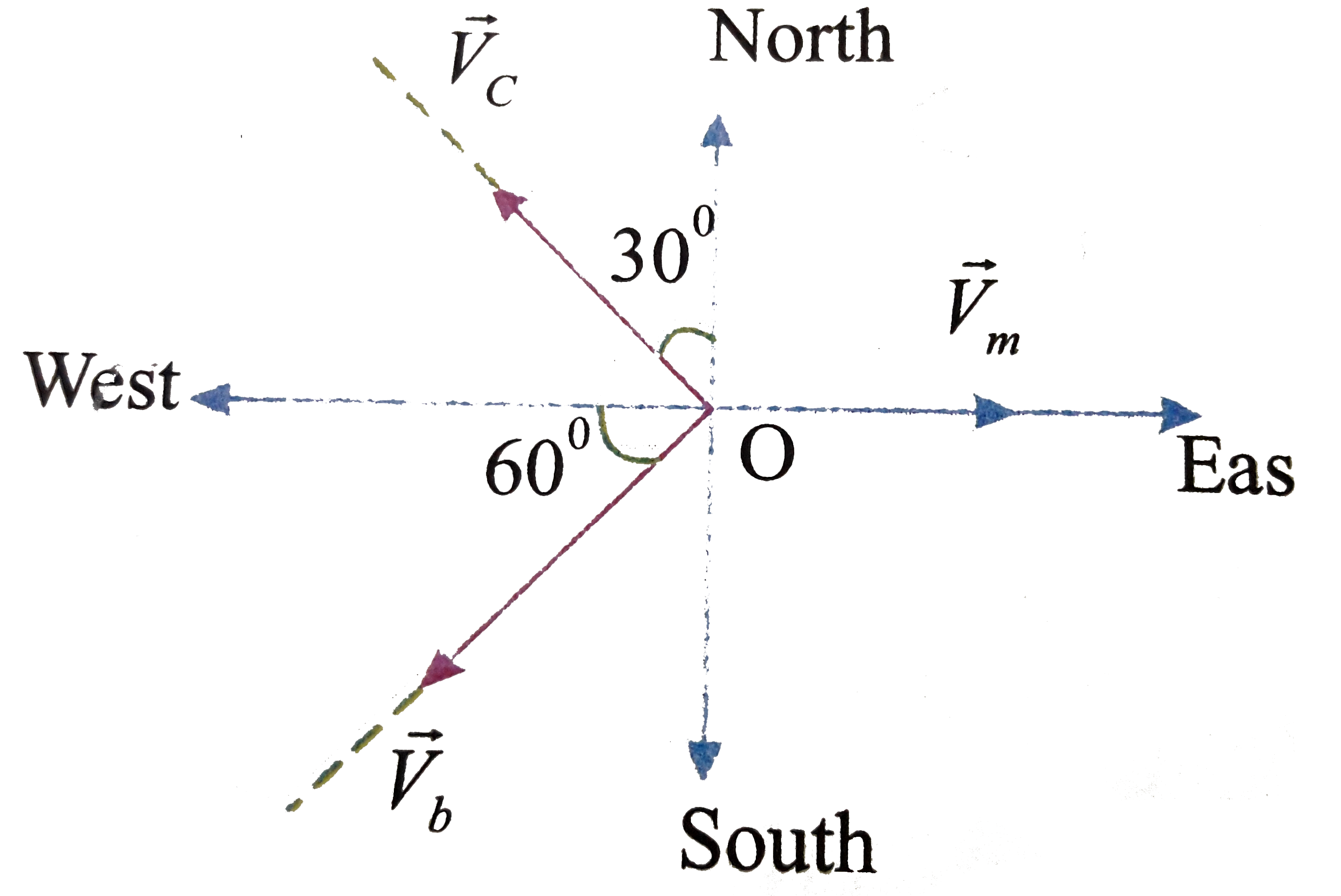
View Solution

