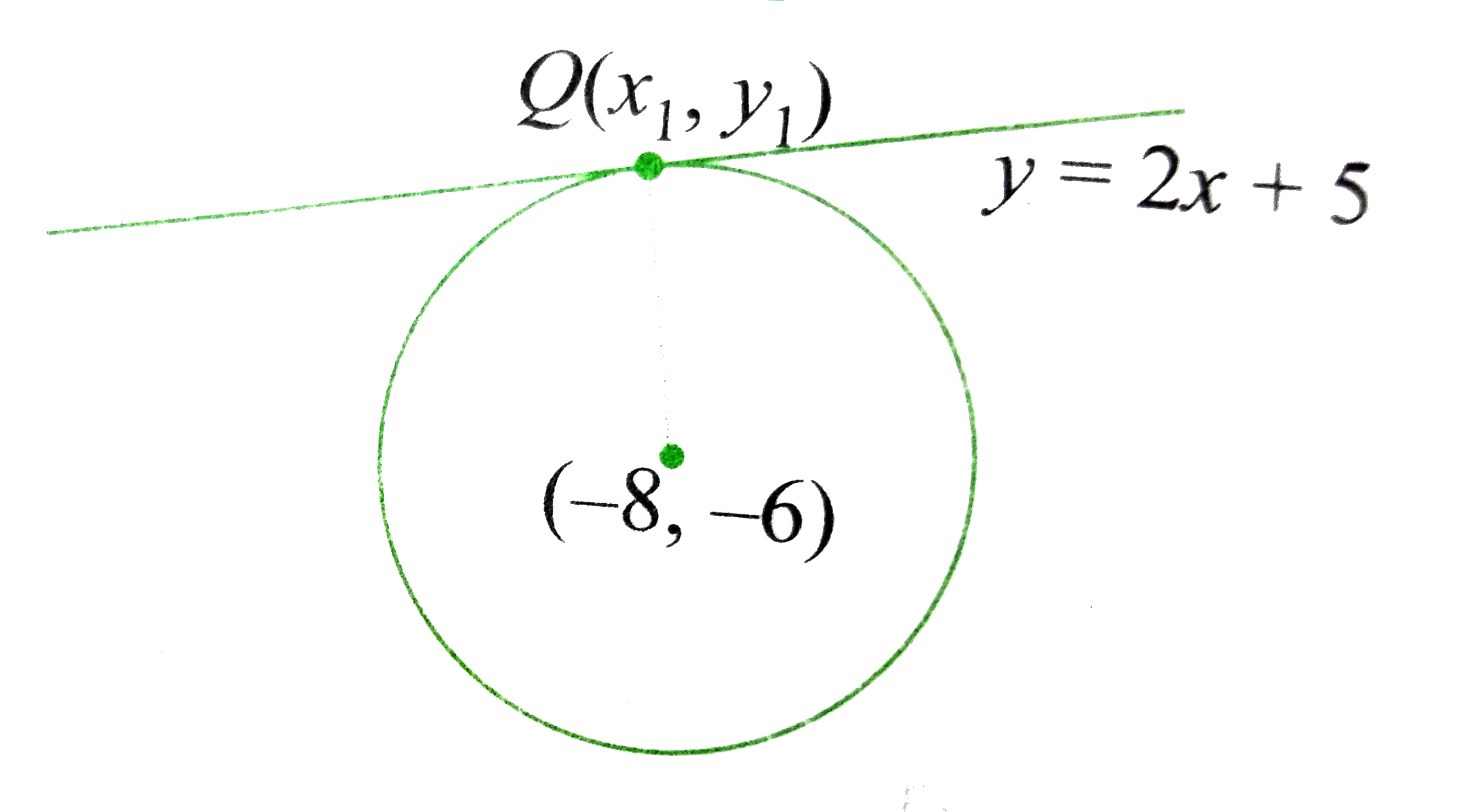
S straight line with slope 2 and y-intercept 5 touches the circle x2+y2=16x+12y+c=0 at a point Q . Then the coordinates of Q are
(−6,11)
(−9,−13)
(−10,−15)
(−6,−7)
The correct Answer is:4
From the figure , we have
y1=2x1+5
y1+6
and y1+6x1+8×2=−1
x1+2y1+20=0
∴x1=−6 and y1=−7
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Multiple)
Explore 25 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Comprehension)
Explore 46 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.6
Explore 5 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
S straight line with slope 2 and y-intercept 5 touches the circle x2+y2=16x+12y+c=0 at a point Q . Then the coordinates of Q are (−6,11) (b) (−9,−13) (−10,−15) (d) (−6,−7)
View SolutionA straight line with slope 2 and y-intercept 5 touches the circle x2+y2+16x+12y+c=0 at a point Q. Then the coordinates of Q are (−6,11) (b) (−9,−13) (−10,−15) (d) (−6,−7)
View Solution
Knowledge Check
Tangent to the curve y=x2+6 at a point P(1, 7) touches the circle x2+y2+16x+12y+c=0 at a point Q. Then the coordinates of Q are
A(−6,−11)B(−9,−13)C(−10,−15)D(−6,−7)The condition for a line y=2x+c to touch the circle x2+y2=16 is
AC=10Bc2=80CC=12Dc2=64The condition for a line y = 2x + c to touch the circle x2+y2=16 is
Ac=10Bc2=80Cc=12Dc2=64
Tangent to the curve y=x2+6 at a point (1,7) touches the circle x2+y2+16x+12y+c=0at a point Q, then the coordinates of Q are (A) (−6,−11) (B) (−9,−13) (C) (−10,−15) (D) (−6,−7)
View SolutionFind the slope and y-intercept of the liney=−2x+3.
View SolutionA line with gradient 2 is passing through the point P(1,7) and touches the circle x2+y2+16x+12y+c=0 at the point Q. If (a, b) are the coordinates of the point Q, then find the value of (7a+7b+c).
View SolutionThe straight line xcosθ+ysinθ=2 will touch the circle x2+y2−2=0 if
View SolutionA line with gradient 2 is passing through the point P(1, 7) and touches the circle x2+y2+16x+12y+c=0 at the point Q. If (a,b) are the coordinates of the point Q, then find the value of (7a+7b+c)
View Solution

