Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
Given in ΔABC ,AD is a median
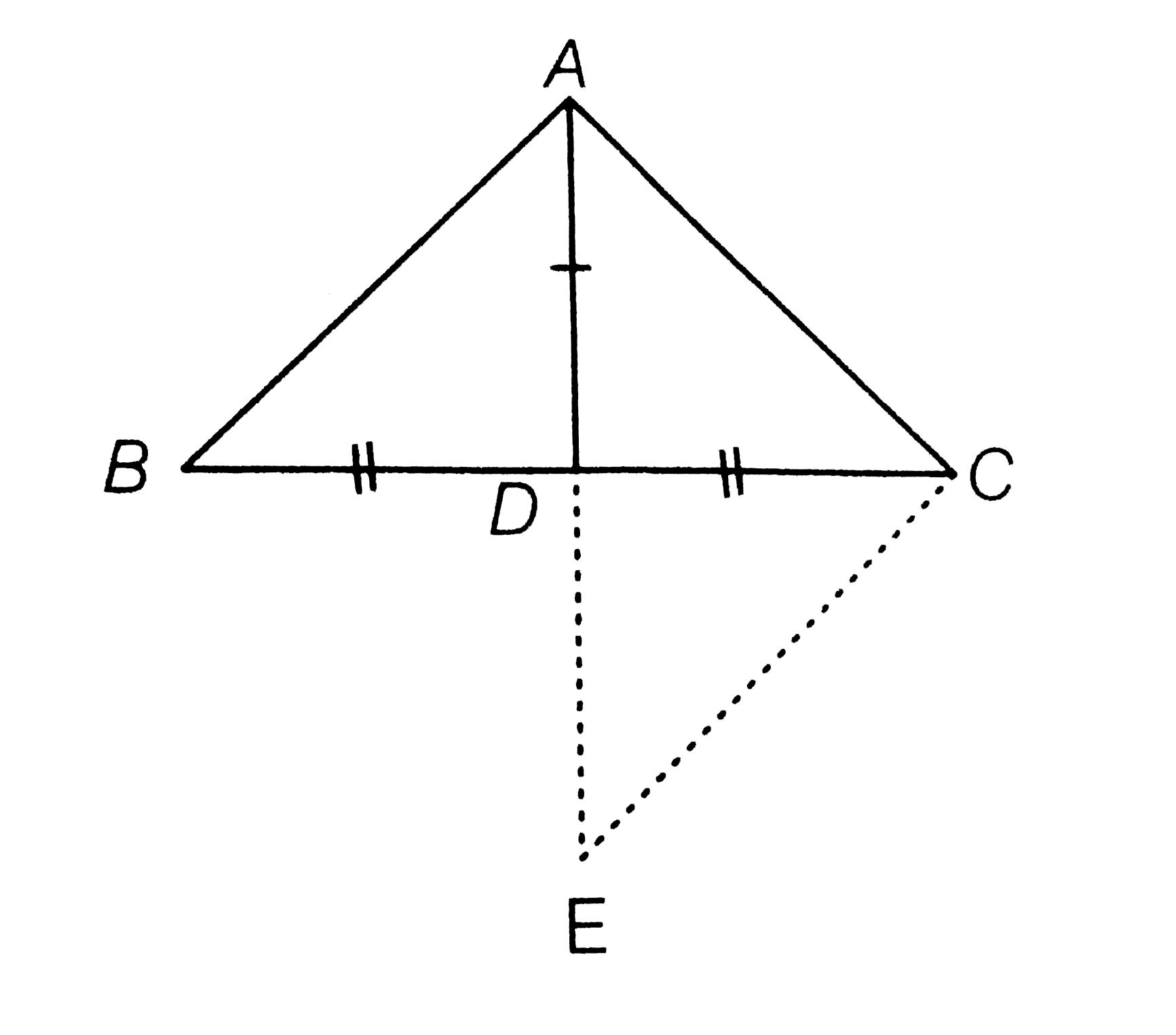
Constrution
Produce AD to a point E such that AD=DE and join CE
TP prove AC+AB>2AD
Proof in ΔABDandΔECD
AD =DE [by construction ]
BD =CD [given AD is the median ]
a∩g≤ADB=∠CDE [vertically opposite angle ]
∴ΔABD≅ΔECD [by SAS congruence rule ]
⇒AB=CE [by CPCT ]
Now in ΔAEC,
AC+EC>AE [Sum of two sides of a triagle is grater than the third side ]
∴AC+AB>2AD [from Eq. (i) and also taken that AD=AE ]
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS11videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS8videos
VOLUME AND SURFACE AREA
Similar Questions
Which of the following statements are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side. GIVEN : △ABC in which AD is a median. PROVE : AB+AC>2AD CONSTRUCTION : Produce AD to E such that AD=DE. Join EC.
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side.
View SolutionTheorem 7.8 : The sum of any two sides of a triangle is greater than the third side.
View SolutionProve that the perimeter of a triangle is greater than the sum of its three medians.
View SolutionIf two sides of a triangle are ˆi+2ˆjandˆi+ˆk, then find the length of the third side.
View SolutionProve that the sum of the sides of a quadrilateral is greater than twice of one of its diagonal.
View SolutionIf two side of a triangle are ˆi+2ˆjandˆi+ˆk , then find the length of the third side.
View SolutionShow that the difference of any two sides of a triangle is less than the third side.
View SolutionTheorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
View Solution


