In the adjoining figure, AB = AC: CP||BA and AP is the bisector of ∠CAD. Prove that
(i) ∠PAC=∠BCAand
(ii) ABCP is a parallelogram.
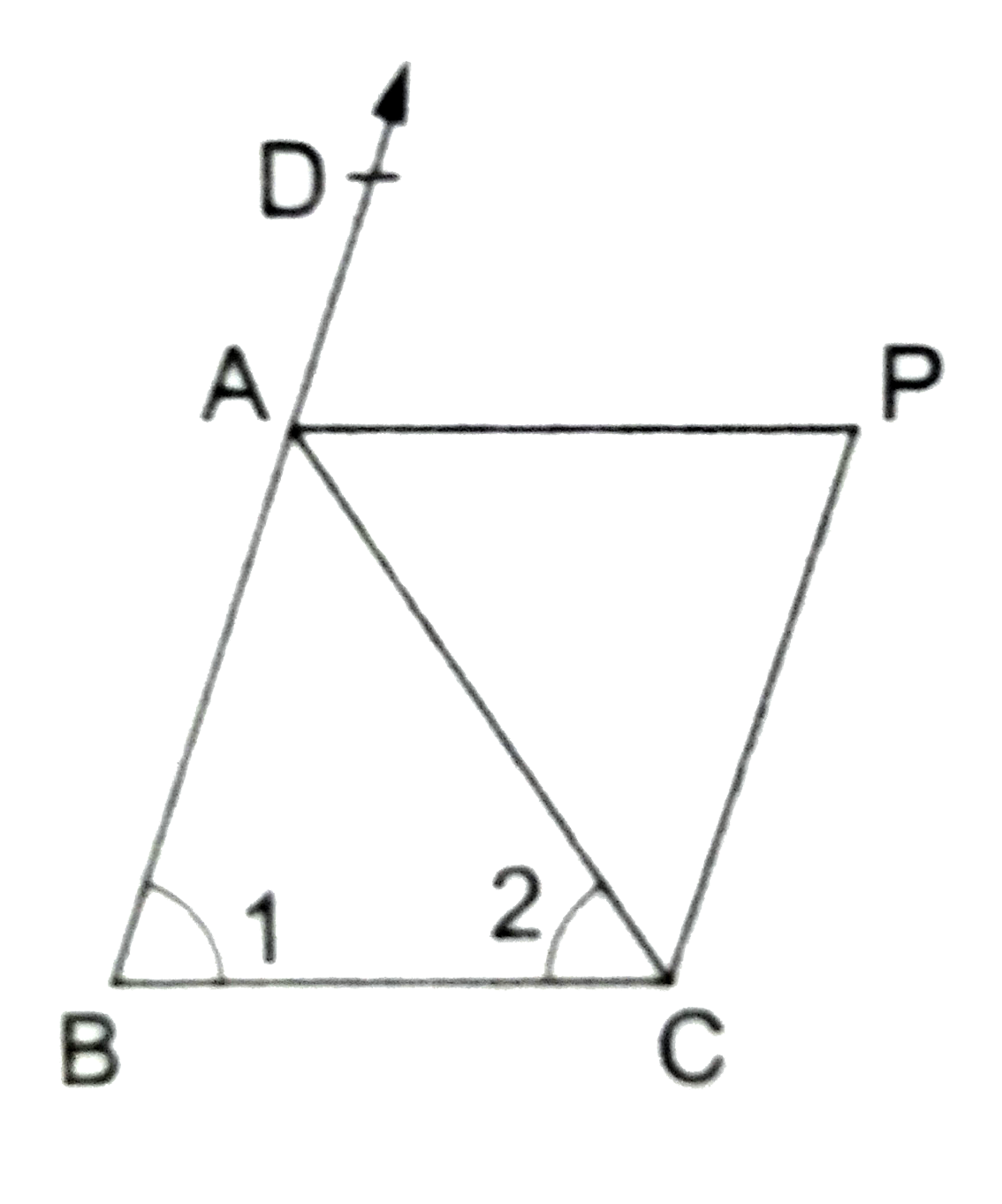
In △ABC,AB=AC⇒∠1=∠2.
Ext. ∠CAD=∠1+∠2
⇒∠CAD=2(∠2) [∵∠1=∠2]
⇒2∠PAC=2(∠2)⇒∠PAC=∠2⇒∠PAC=∠BCA.
Now , ∠PAC=∠BCA⇒AP∣∣BC (∵∠PACand∠BCA are alt. interior ∠)
Also, CP||BA (given).
∴ ABCP is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Matching of Columns:
Explore 2 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
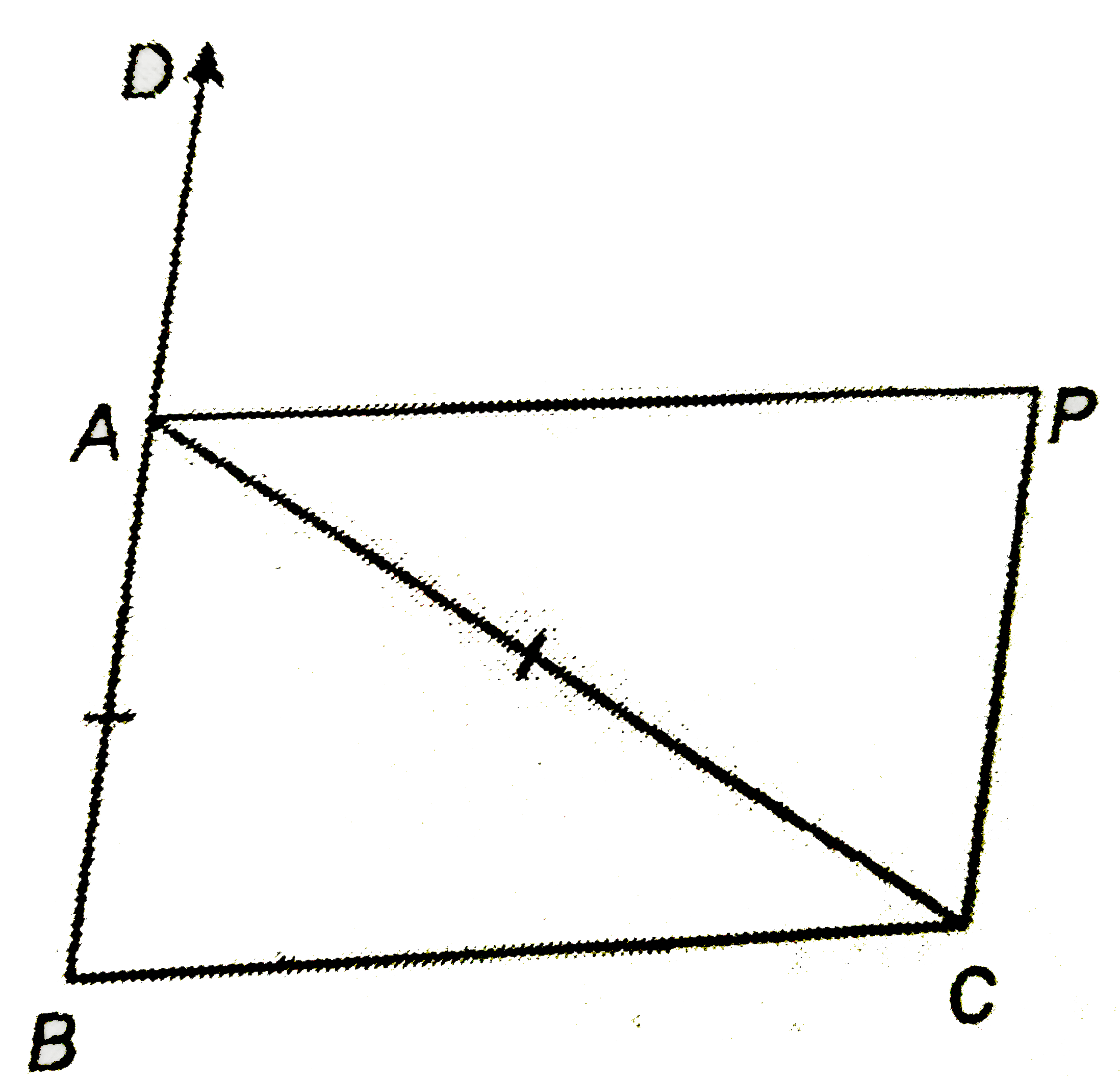
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View Solution
Knowledge Check
In the adjoining figure CD is perpendicular on AB. CN is the angle bisector of ∠ACB.∠ACN=50∘,∠NCD is:
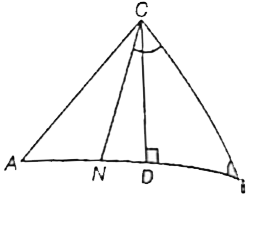 AA)13∠ACBBB)∠CAB−∠CBACC)12(∠CBA−∠BAC)DD)can't be determined
AA)13∠ACBBB)∠CAB−∠CBACC)12(∠CBA−∠BAC)DD)can't be determined
In the figure, AD is the bisector of angle BAC. Prove that AB>BD.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
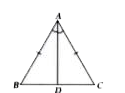
∠B=∠C
View SolutionIn the given figure , AB=CD,CE=BF and ∠ACE=∠DBF . Prove that
△ACE≅△DBF
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
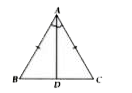
BD = CD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
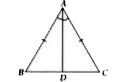
AD⊥BC
View SolutionIn the given figure , AC>AB and AD bisects ∠BAC Prove that ∠ADC>ADB
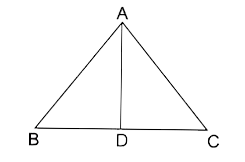
View SolutionIn the given figure, AP is perpendicular to BC, and AQ is the bisector ∠PAC. What will be the measure of ∠PAQ?
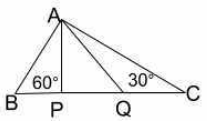
View Solution

