If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is
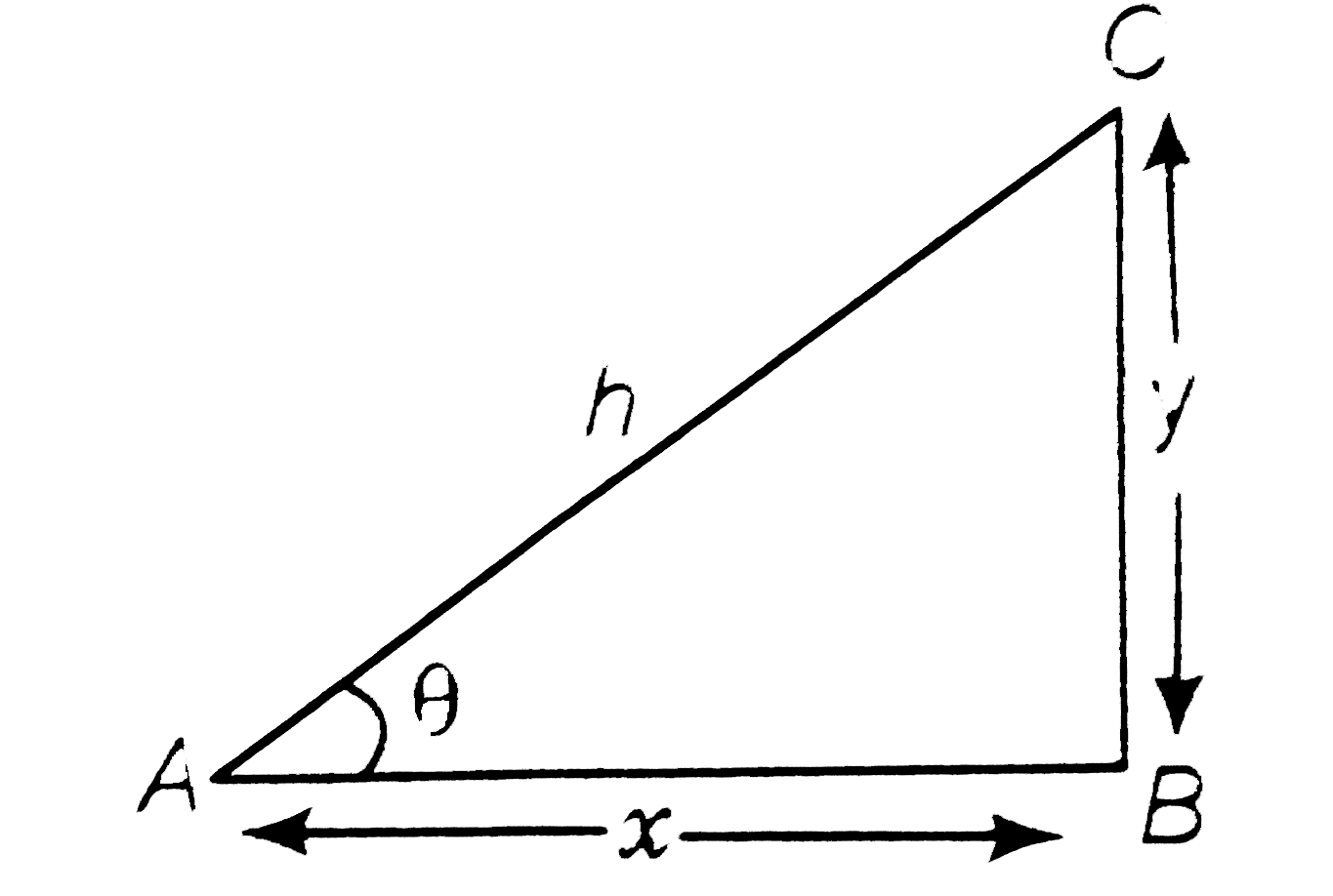
Let ABC be a triangle with AC =h, AB=x and BC=y.
Also,
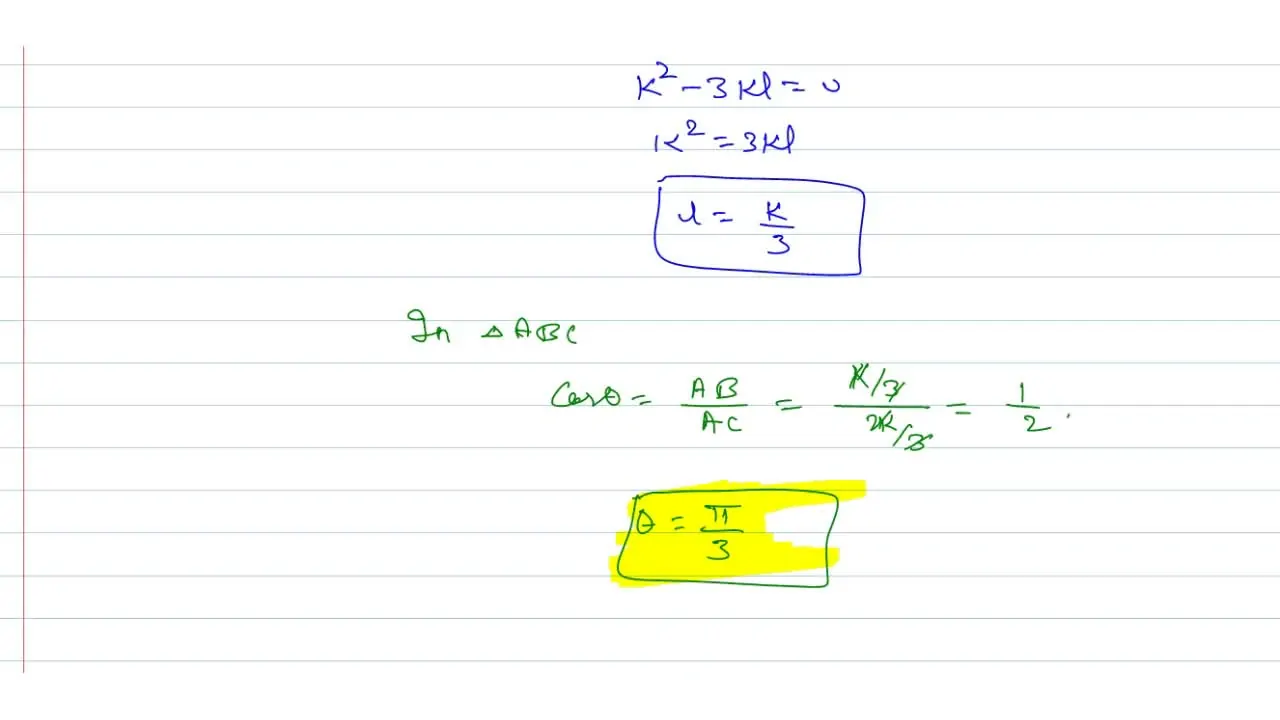
Let h+x=k
[Using eq.]
...............(i)
Also, area of
Since, ..............(ii)
.............(iv)
............(v)
For ,
[positive]
or [not possible]
Again, differentiating w.r.t in Eq. (v), we get
Which is less than zero.
Hence, area of the right angled triangle is maximum, when the angle between them is .
Related Playlists
Similar Questions
If the sum of the lengths of the hypotenues and a side of a right angled triangle is given, show that the area of the triangle is maximum when the angle between them is π/3 .
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
View SolutionIf the sum of a side and hypotenuse of a right angled triangle is given then show that area of triangle will be maximum when the angle between side and the hypotenuse is π/3.
View SolutionIf the length of the hypotenuse of a right angled triangle is 10 cm, then what is the maximum area of such a right angled triangle?
View SolutionThe maximum area of a right angled triangle with hypotenuse h is
View SolutionIn the right triangle BAC,∠A=π2anda+b=8. The area of the triangle is maximum when ∠C , is
View SolutionThe hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
View SolutionProve that the perimeter of a right-angled triangle of given hypotenuse is maximum when the triangle is isosceles
View SolutionFind the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
View Solution