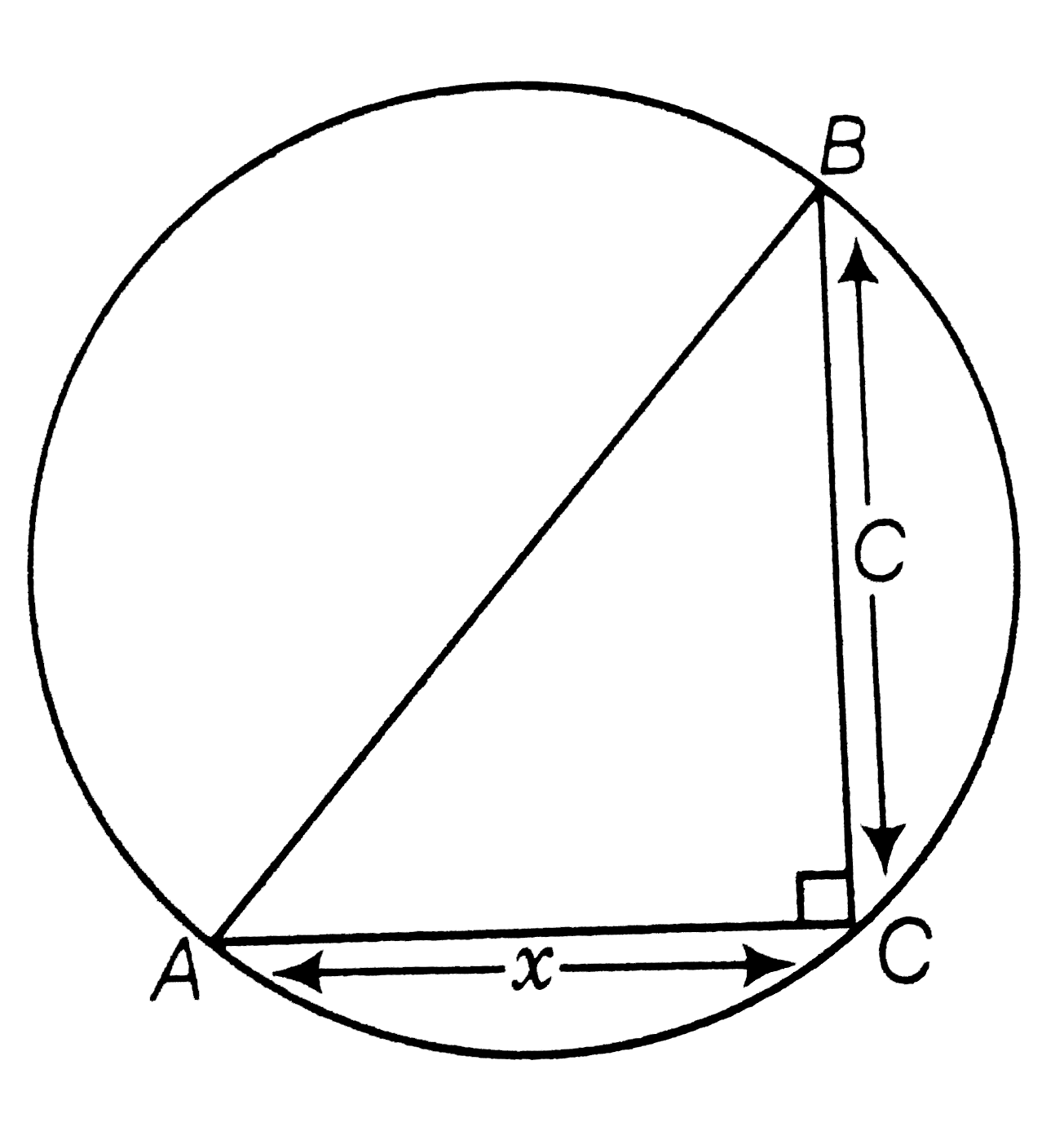
is a diameter of a circle and is any point on the circle. Show that the area of is maximum, when it is isosceles.
We have, AB=2r
and [since, angle in the semi-circle is always ]
Let AC=x and BC=y
……………………(i)
Now, area of
[using Eq. (i)]
Now, differentiating both sides w.r.t. x, we get
Now,
x
Again, differentiating both sides, w.r.t. x, we get
For , the area of triangle is maximum.
For ,
Since,
Hence, the triangle is isosceles.
Related Playlists
Similar Questions
AB is a diameter of a circle and C is any point on the circle. Show that the area of ABC is maximum, when it is isosceles.
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then (a) the area of ΔABC is maximum when it is isosceles (b) the area of ΔABC is minimum when it is isosceles (c) the perimeter of ΔABC is minimum when it is isosceles (d) none of these
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionIf A(3,−4),B(7,2) are the ends of a diameter of a circle and C is a point on the circle then the circumcentre of ABC is
View SolutionIf diameter of a circle is 2r cm, then area of the circle is :
View SolutionIf diameter of a circle is r cm, then the area of a circle is :
View SolutionIf A(3,-4), B(7,2) are the ends of a diameter of a circle and C(3,2) is a point on the circle then the orthocentre of the ΔABC is
View SolutionIf diameter of a circle is r2cm, Then the area of a circle is :
View SolutionIn figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
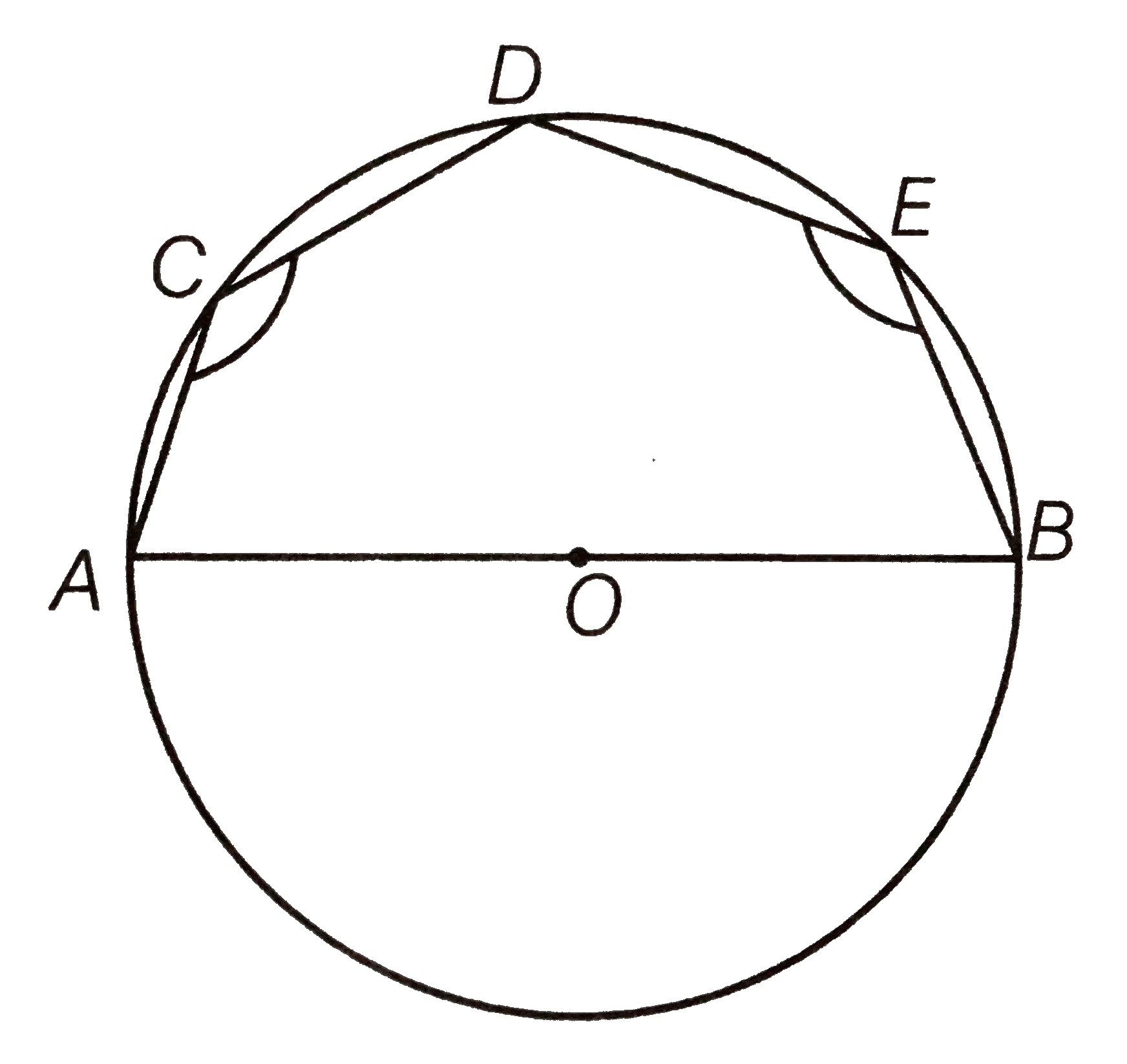 View Solution
View Solution


