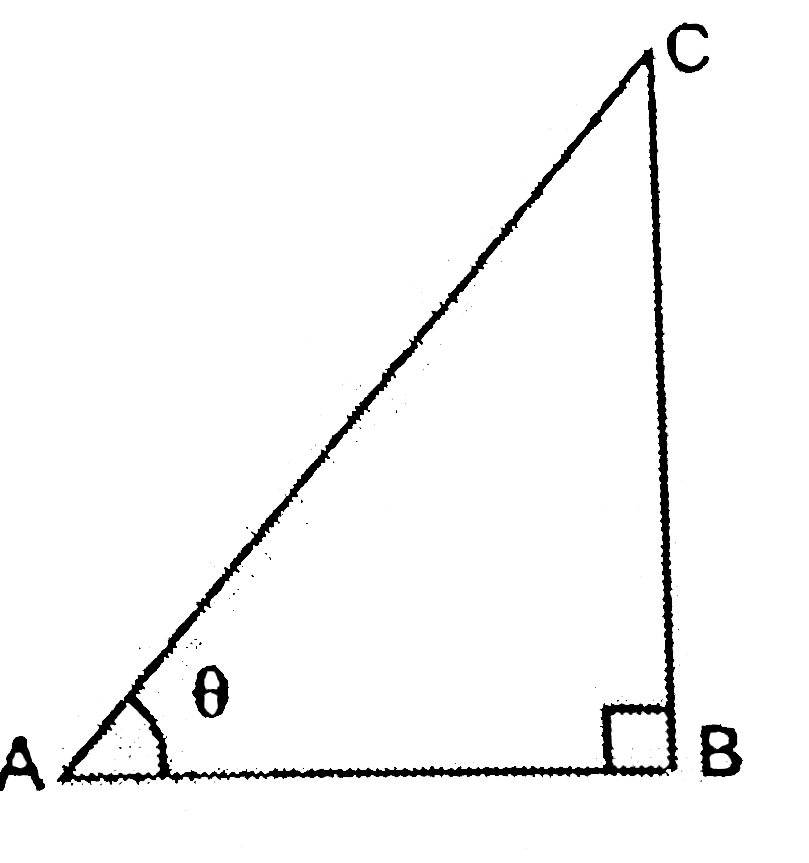
If the sum of a side and hypotenuse of a right angled triangle is given then show that area of triangle will be maximum when the angle between side and the hypotenuse is $π / 3$ .

Video Solution

Text Solution

Verified by Experts

Let, In $Δ A B C, ∠ B = 90^{\circ}$
Let AB = x and AC = y
Then x+y = k
Which is given a constant.
$B C = \sqrt{A C^{2} - A B^{2}}$
$= \sqrt{y^{2} - x^{2}}$
$= \sqrt{{(k - x)}^{2} - x^{2}}$
$= \sqrt{k^{2} - 2 k x}$
$Now area of Δ A B C$
$Δ = \frac{1}{2} \times A B \times B C$
$= \frac{1}{2} \times x \times \sqrt{k^{2} - 2 k x}$
$\Rightarrow Δ^{2} = \frac{1}{4} x^{2} (k^{2} - 2 k x)$
Let $Δ^{2} = S$ ,
$∴ S = \frac{1}{4} k (k x^{2} - 2 x^{3})$
$\Rightarrow \frac{d S}{d x} = \frac{1}{4} k (2 k x - 6 x^{2})$
For maxima/minima
$\frac{d S}{d x} = 0$
$\Rightarrow 2 k x - 6 x^{2} = 0$
$\Rightarrow x = \frac{k}{3}$
and $\frac{d^{2} S}{{d x}^{2}} = \frac{1}{4} k (2 k - 12 x)$
$at x = \frac{k}{3}$
$\frac{d^{2} S}{{d x}^{2}} = \frac{1}{4} k (2 k - 4 k) = - \frac{k^{2}}{2} < 0$
$∴ At x = \frac{k}{3}, \cdot$ S is maximum
$\Rightarrow At x = \frac{k}{3}, Δ^{2}$ is maximum
$\Rightarrow At x = \frac{k}{3}, Δ$ is maximum
and $y = k - \frac{k}{3} = \frac{2 k}{3}$
If $∠ B A C = θ,$ then
$cos θ = \frac{A B}{A C} = \frac{x}{y} = \frac{k / 3}{2 k / 3} = \frac{1}{2}$
$\Rightarrow θ = π / 3$ $π / 3$ for maximum area.

Updated on:21/07/2023

If the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is $\frac{π}{3} .$
A $\frac{π}{12}$
B $\frac{π}{4}$
C $\frac{π}{3}$
D $\frac{π}{2}$
The hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
A5 $c m^{2}$
B6.25 $c m^{2}$
C6.5 $c m^{2}$
D12.5 $c m^{2}$