Two inclined frictionless tracks, one gradual and the other steep meet at a from where two stones are allowed to slide down from rest, one on each track as shown in Figure. Which of the following statement is correct ?
 .
.
Both the stones reach the bottom at the same time but not with the same speed.
Both the stones reach the bottom with the same speed and stone I reaches the bottom earlier than stone II.
Both the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.
Both the stones reach the bottom at different times and with different speeds
The correct Answer is:C
In figure, AB and AC are two smooth planes inclined to the horizontal at ∠θ1and∠θ2 respectively.
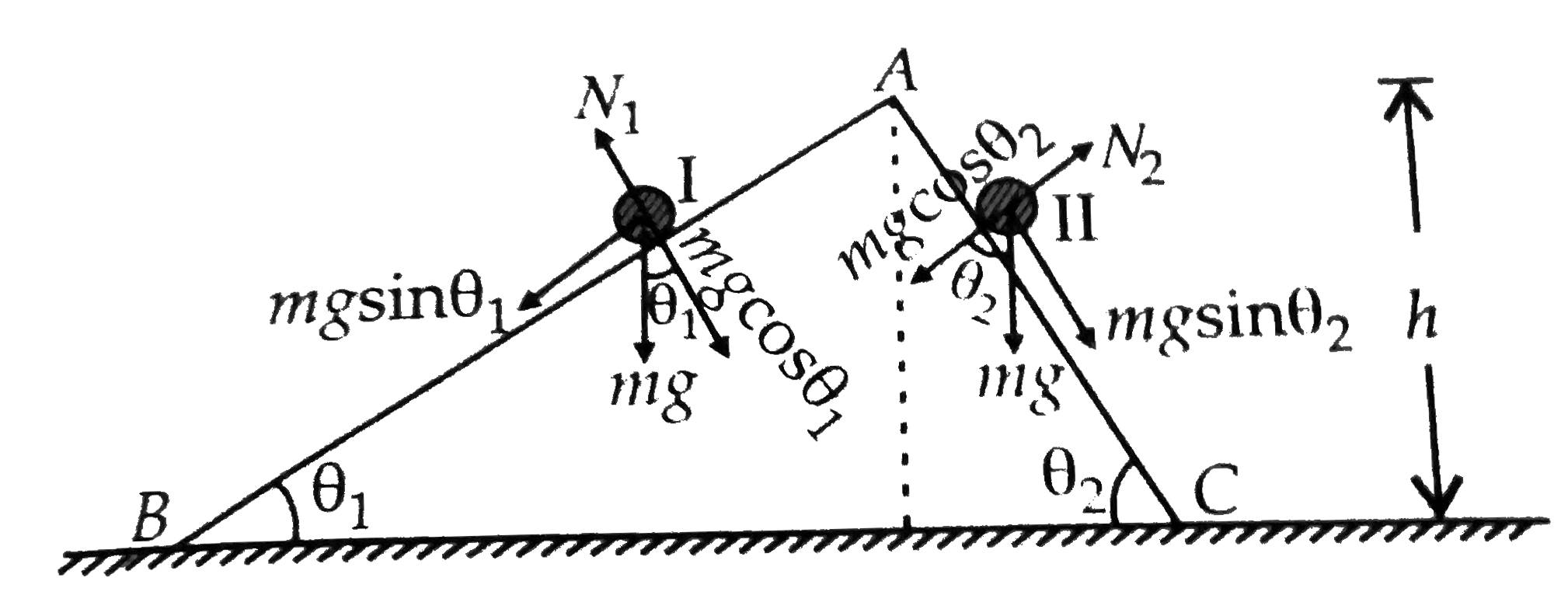
As height of both the planes is the same, therefore, both the stones will reach the bottom with same speed.
According to law of conservation of mechanical energy
PE at the top = KE at the bottom
∴mgh=12mv21...(i)
and mgh=12mv22...(ii)
From (i) and (ii) , we get v1=v2
As is clear from figure, acceleration of the two stones are a1=gsinθ1 and a2=gsinθ2 respectively.
As θ2>θ1 ∴ a2>a1
From v=u+at=0 + at or t=va
As t∝1a, and a2>a1∴t2<t1
Hence, stone II will take lesser time and reach the bottom earlier than stone I.
Topper's Solved these Questions
- WORK , ENERGY AND POWERBook:NCERT FINGERTPS ENGLISHChapter:WORK , ENERGY AND POWERExercise:ASSERTION & REASON
Explore 15 Videos
- WORK , ENERGY AND POWERBook:NCERT FINGERTPS ENGLISHChapter:WORK , ENERGY AND POWERExercise:Motion Of Work And Kinetic Energy : The Work-Energy Theorem
Explore 4 Videos
- WORK , ENERGY AND POWERBook:NCERT FINGERTPS ENGLISHChapter:WORK , ENERGY AND POWERExercise:Assertion And Reason
Explore 15 Videos
- WAVESBook:NCERT FINGERTPS ENGLISHChapter:WAVESExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
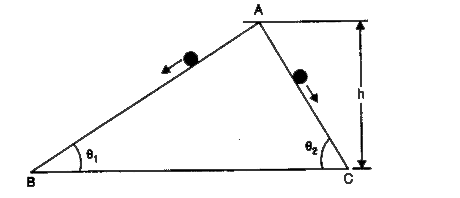
Two inclined frictionless tracks, one gradual and the other steep meet at A from where to stones are allowed to slide down from rest, one on each track (fig.) Will hte stones reach the bottom at the same time? Will they reach there with the same speed? Explain, given θ1=30∘, θ92)=60∘ and h=10m. What are the speeds and time taken by the two stones?
View SolutionIn the circuit shown in the figure, which one of following statement is correct

View SolutionTwo strings , one thick and other thin are connected as shown in Fig. 7.89.
Which of the following statement(s) is correct with regard to above arrangement?

View SolutionTwo wheels A and B are released from rest from points X and Y respectively on an inclined plane as shown in the figure. Which of the following statement(s) is/are incorrect?
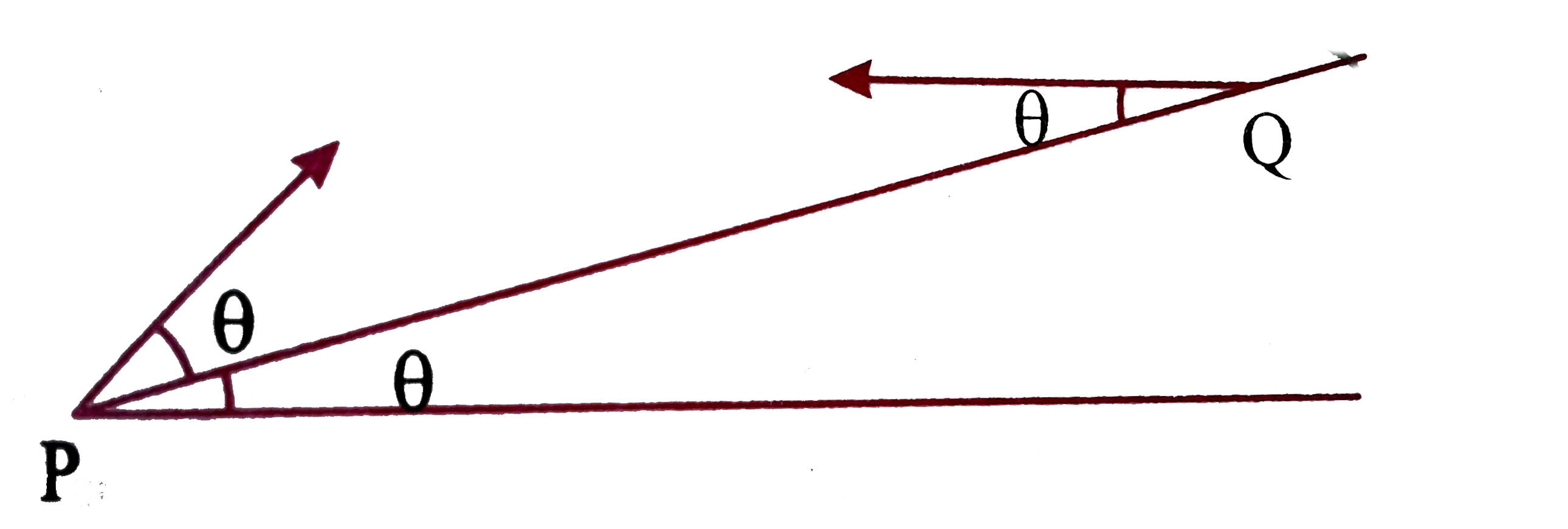
View SolutionFrom an inclined palne two particles P,Q are projected with same speed at same angle θ,one up and other down the plane as shown in figure.Which of the following statement(s) is/are correct ?
View SolutionIf the B-H curves of two samples of P and Q of iron are as shown below, then which one of the following statements is CORRECT?
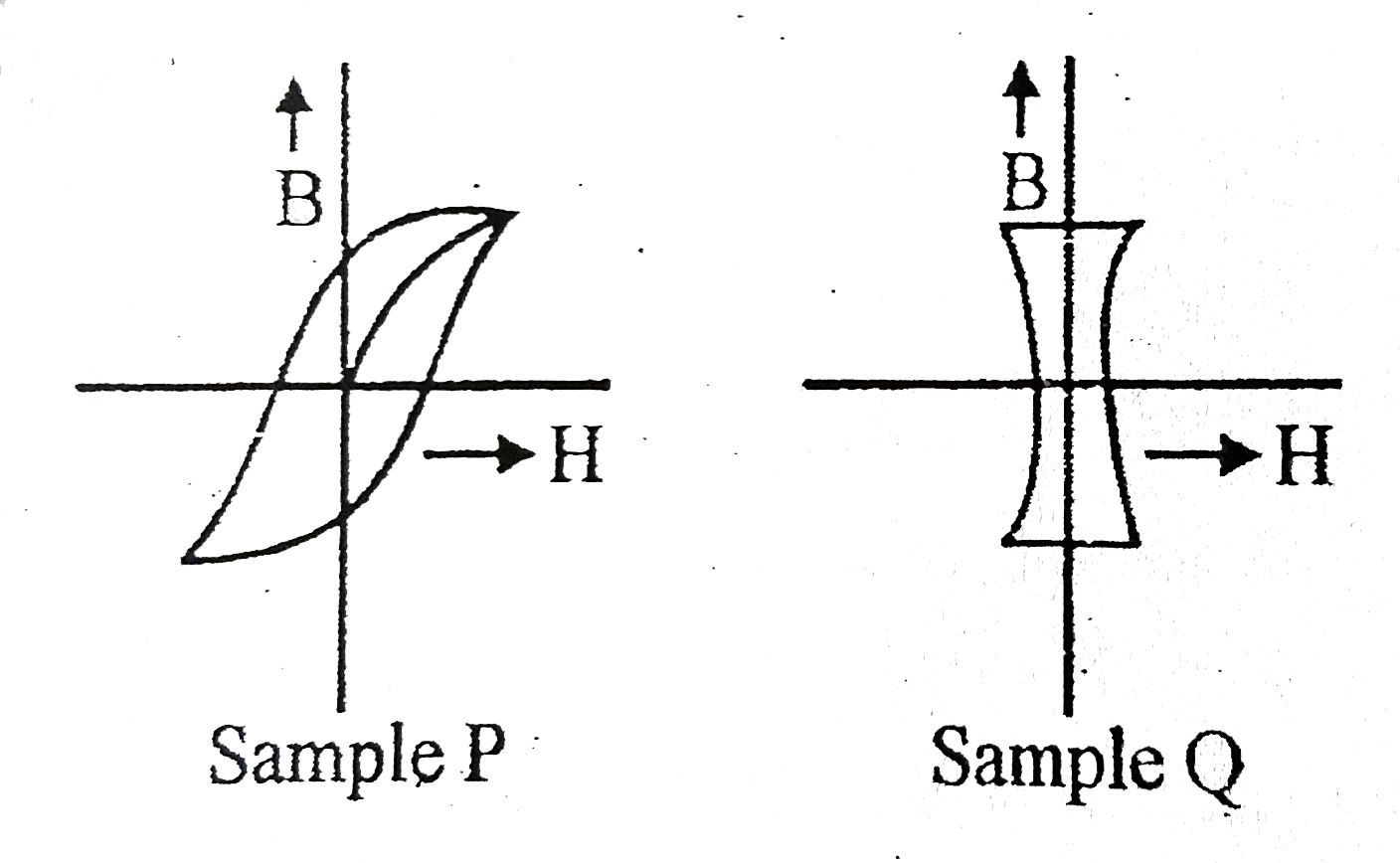
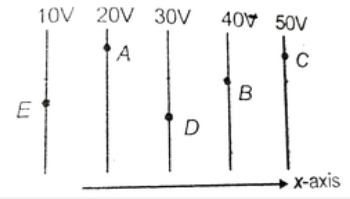
View SolutionFigure shows a set of equipotential surfaces. There are a few points marked on them. An electron is being moved from one point to other. Which of the following statements is / are correct ?
View SolutionA block slides down a smooth inclined placne when released from the top, while another falls freely from the same point. Which of the following is/are correct ?
View SolutionA velocity-time graph of two vehicals A & B starting from rest at the same time is given in the figure. The statements which is correct from graph.

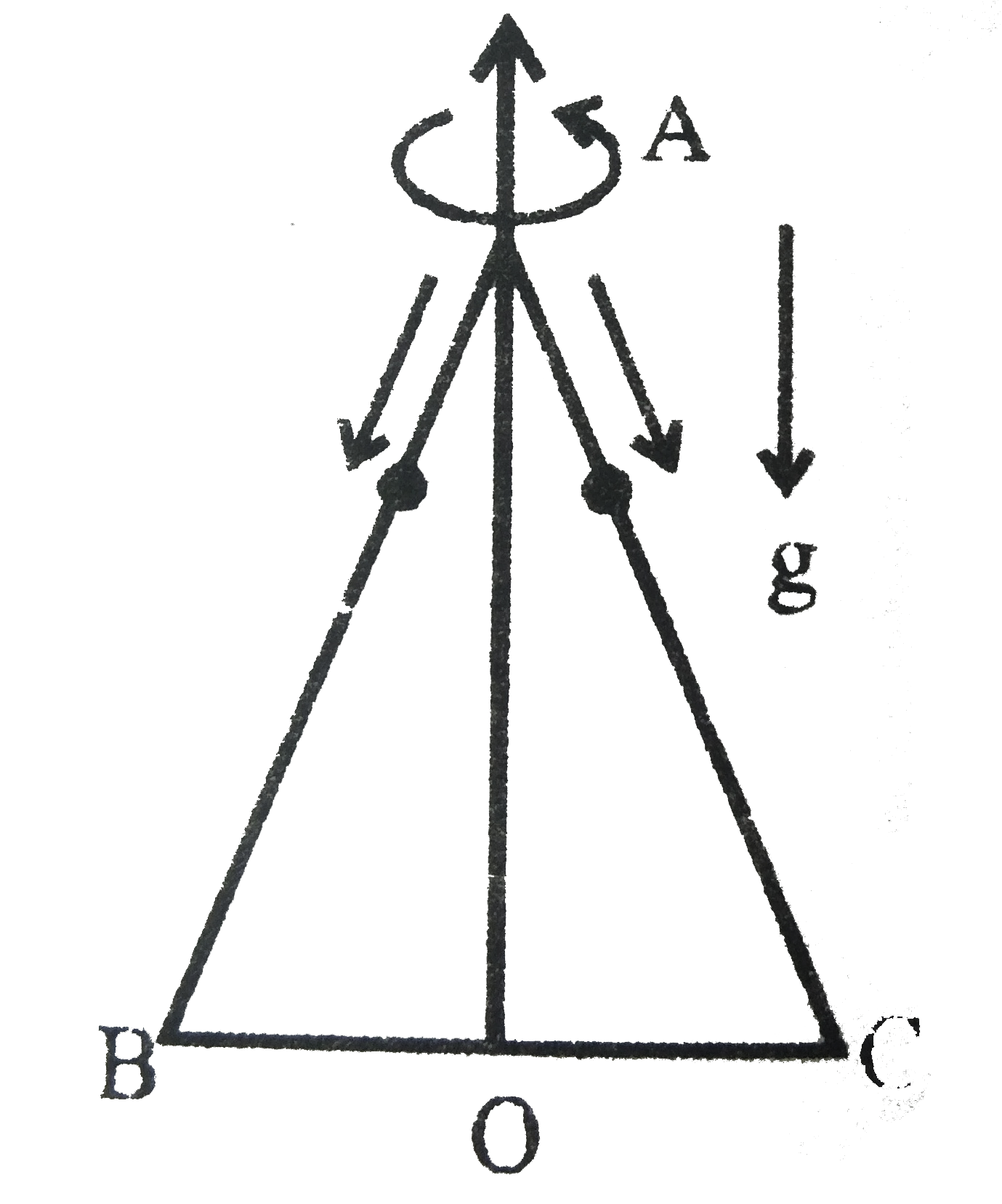
View SolutionA equilaterial triangle ABC formed from a uniform wire has two small identical beads initially located at A. The triangle is set rotating about the vertical axis AO. Then the beads are released from rest simultaneously and allowed to slide down. one long. AB and the other along AC as shown. Neglecting frictional effects, the quantities that are conserved as the beads slide down, are.
 .
.
View Solution

