Question

The potential energy function for a particle executing linear SHM is given by ${\displaystyle V\left(x\right)=\frac{1}{2}k{x}^2}$ where k is the force constant of the oscillator. For ${\displaystyle k=0.5N{m}^{-1}}$, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches ${\displaystyle x=\pm x_m}$.if V and K indicate the potential energy and kinetic energy respectively of the particle at ${\displaystyle x=+x_m}$,then which of the following is correct?

Options

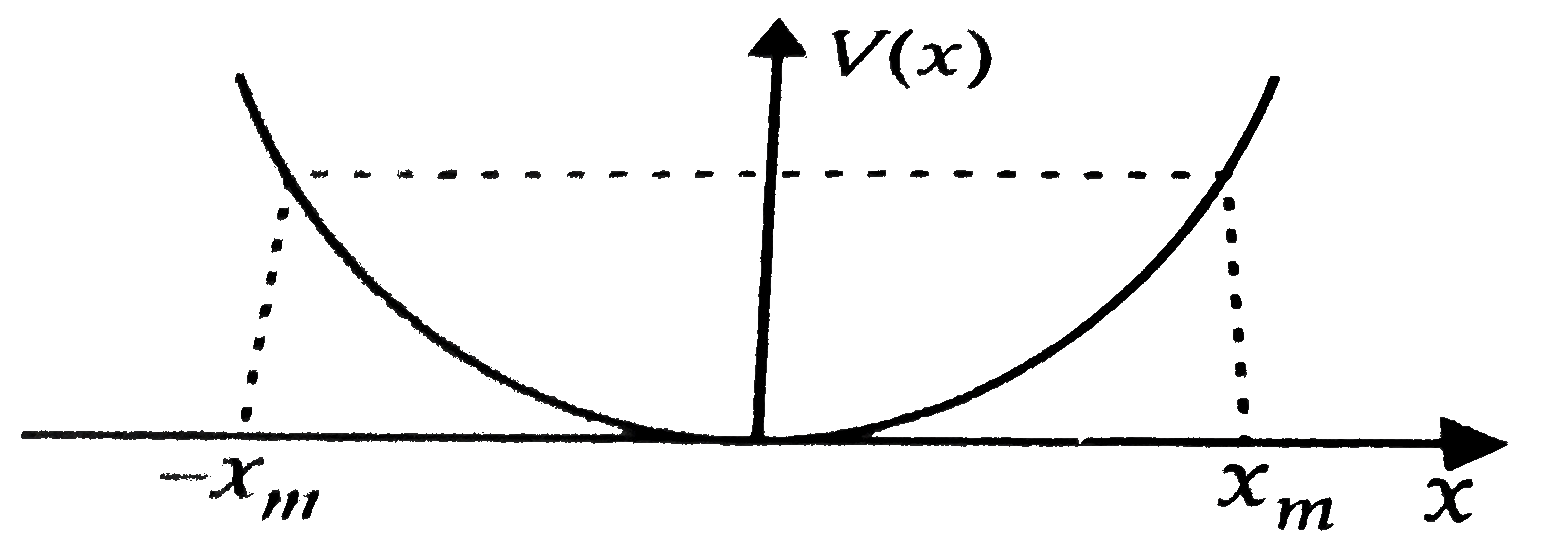
A. V=0, K=E
B. V=E, K=0
C. V lt K, K=0
D. V=0, K lt E

Answer

B

Explanation

At any instant, the total energy of an oscillator is the sum of kinetic energy and potential energy.
Total energy, E=K + V
At `x= +x_m`, the particle turns back, therefore its velocity at this point is zero, i.e. v=0
`therefore` K=0
`therefore E=1/2kx^2 =V`