The potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
V=0, K=E
V=E, K=O
V<E, K=O
V=O, K<E
To solve the problem, we need to analyze the potential energy function and the total energy of the particle executing simple harmonic motion.
1. Identify the potential energy function:
The potential energy V(x) is given by:
V(x)=12kx2
where k=12N/m.
2. Substitute the value of k:
Plugging in the value of k into the potential energy function:
V(x)=12(12)x2=14x2
3. Write the expression for total energy:
The total energy E of the particle is given as 1 joule. The total energy is the sum of kinetic energy K and potential energy V:
E=K+V
Thus, we can write:
1=K+V(x)
4. Express kinetic energy in terms of potential energy:
Rearranging the equation gives:
K=1−V(x)
Substituting the expression for V(x):
K=1−14x2
5. Set the condition for kinetic energy:
Since kinetic energy cannot be negative, we have:
1−14x2≥0
6. Solve the inequality:
Rearranging gives:
1≥14x2
Multiplying both sides by 4:
4≥x2
7. Take the square root:
Taking the square root of both sides gives:
2≥|x|
This implies:
−2≤x≤2
8. Conclusion:
The particle must turn back when it reaches x=±2m because at these points, the kinetic energy becomes zero, and the particle cannot move further in that direction.
Summary:
The particle executing simple harmonic motion with a total energy of 1 joule will turn back when it reaches x=±2m.
---
The potential energy V(x) is given by:
V(x)=12kx2
where k=12N/m.
Plugging in the value of k into the potential energy function:
V(x)=12(12)x2=14x2
The total energy E of the particle is given as 1 joule. The total energy is the sum of kinetic energy K and potential energy V:
E=K+V
Thus, we can write:
1=K+V(x)
Rearranging the equation gives:
K=1−V(x)
Substituting the expression for V(x):
K=1−14x2
Since kinetic energy cannot be negative, we have:
1−14x2≥0
Rearranging gives:
1≥14x2
Multiplying both sides by 4:
4≥x2
Taking the square root of both sides gives:
2≥|x|
This implies:
−2≤x≤2
The particle must turn back when it reaches x=±2m because at these points, the kinetic energy becomes zero, and the particle cannot move further in that direction.
The particle executing simple harmonic motion with a total energy of 1 joule will turn back when it reaches x=±2m.
Similar Questions
The total energy of a particle, executing simple harmonic motion is.
where x is the displacement from the mean position, hence total energy is independent of x.
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View Solution
Knowledge Check
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
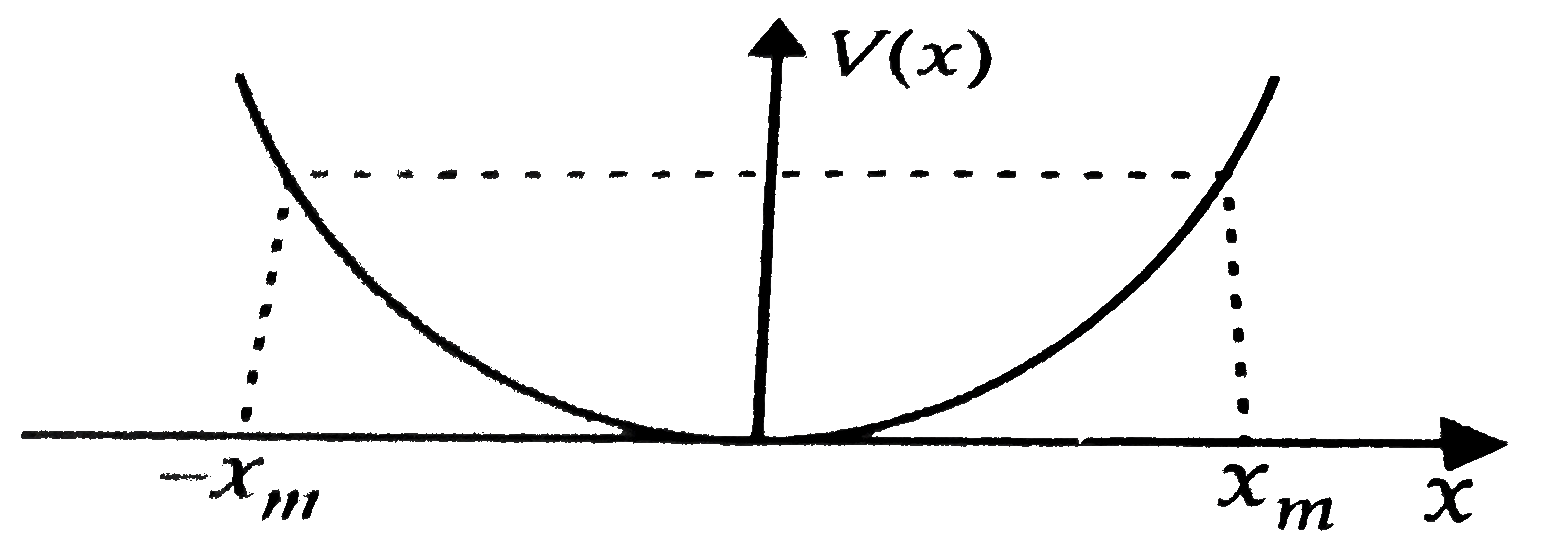 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt EConsider the following statements. The total energy of a particles executing simple harmonic motion depends on its
1. amplitude
2. Period
3. displacement of these :A1 and 2 are correctB2 and 3 are correctC1 and 3 are correctD1, 2 and 3 are correct
The potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionThe potential energy of particle of mass 1kg moving along the x-axis is given by U(x)=16(x2−2x) J, where x is in meter. Its speed at x=1 m is2m/s. Then,
View SolutionTotal energy of a particle executing oscillating motionis 3 joule and given by
E=x2+2x+v2−2v
Where x is the displacement from origin at x=0 and v is velocity of particle at x. Then choose the correct statements)
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View SolutionThe potential energy of a particle of mass m is given by U=12kx2 for x<0 and U = 0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
View Solution
