The work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
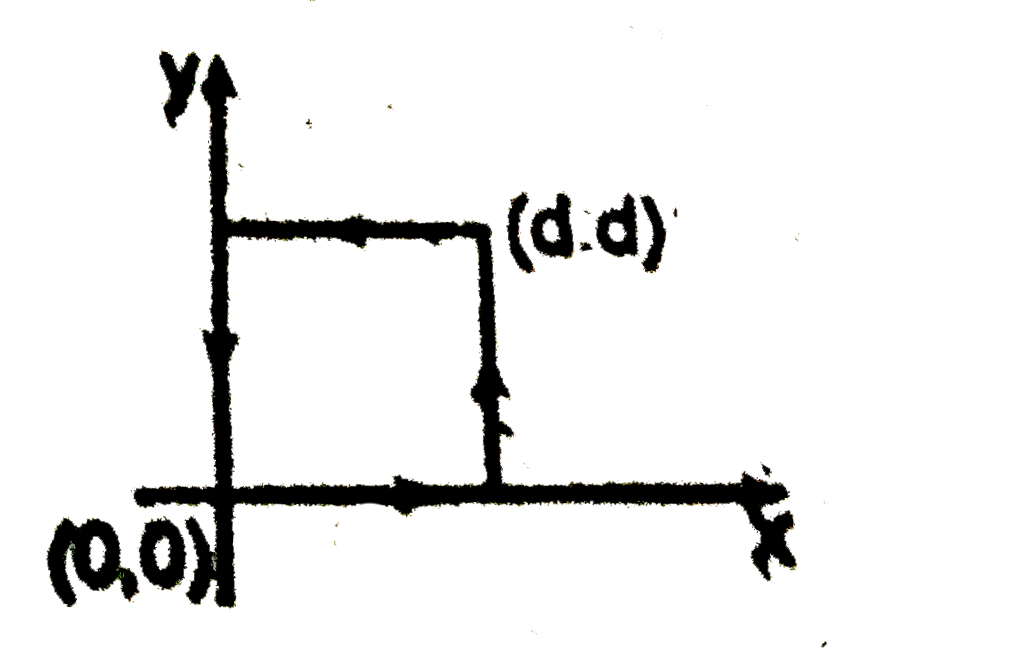
The correct Answer is:D
W=∫¯¯¯F.d¯x=∫A(y2+2x2).(dx+dy)
=A∫(y2dx+2x2dy)
WOA=0+0,WAB=A[0+2d2d]
WBC=A[d2(−d)+0],WCD=A[0+0]
W=0+2Ad3−Ad3+0=Ad3.
Related Playlists
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.268videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.2720videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.249videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
The work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
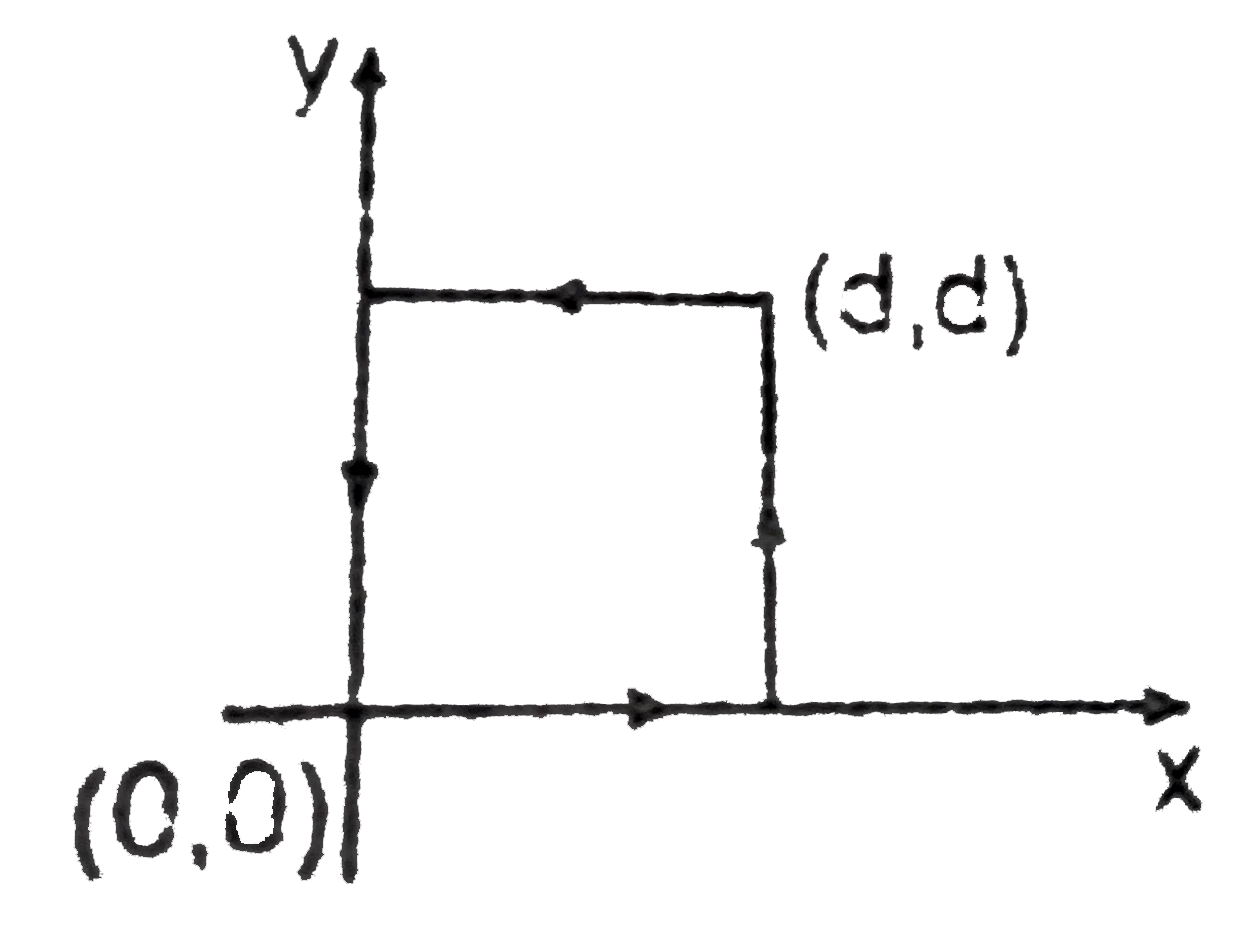 View Solution
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionThe work done by the forces →F=2ˆi−ˆj−ˆk in moving an object along the vectors 3ˆi+2ˆj−5ˆk is:
View SolutionA particle is moved along the different paths OAC,OBC&ODC as shown in the figure . Path ODC is a parabola , y=4x2. Find the work done by a forc →F=xyˆi+x2yˆj on the particle along these paths. Is this force a conservative force ?
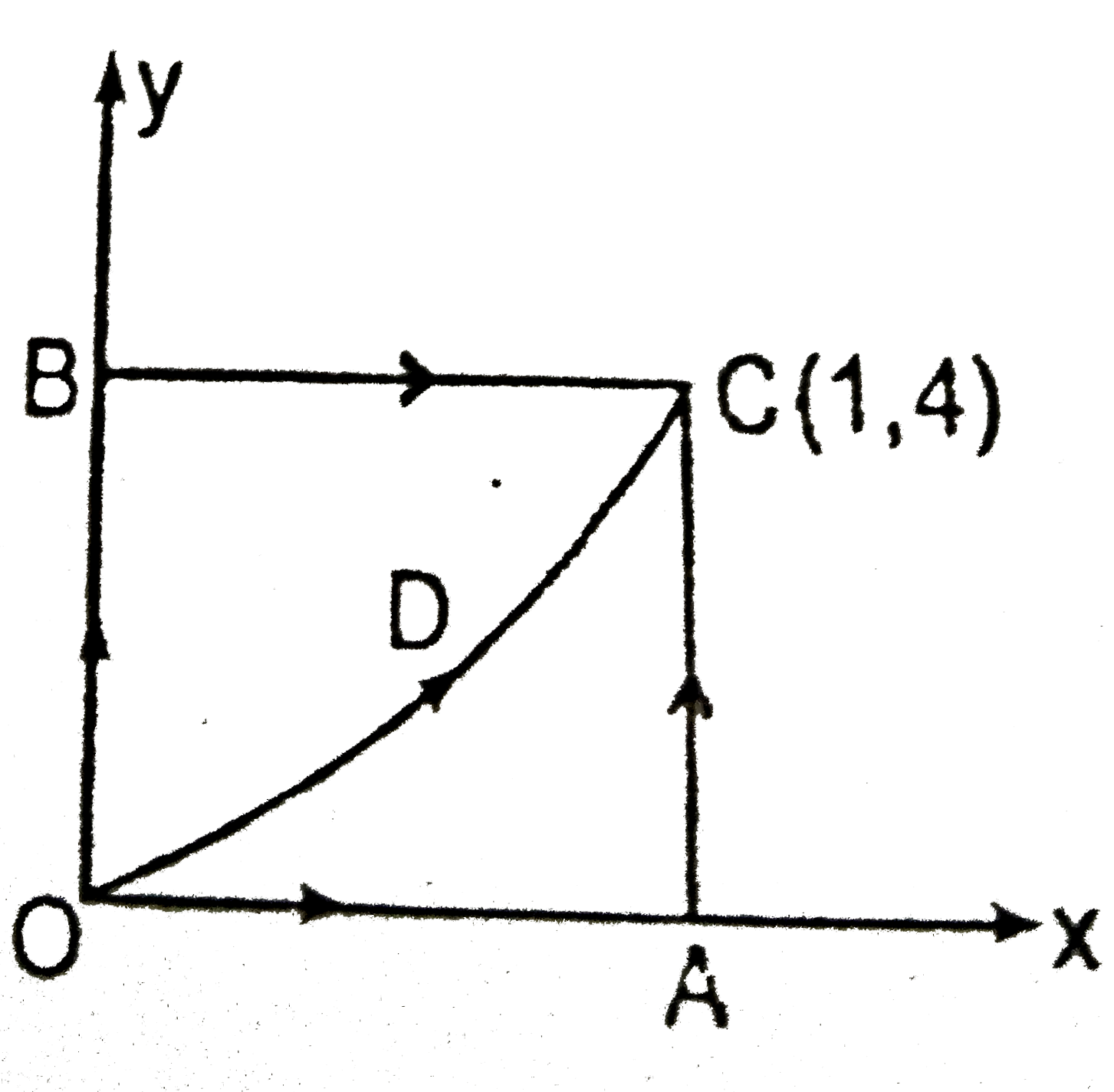 View Solution
View SolutionA particle is moved along a path AB−BC−CD−DE−EF−FA, as shown in figure, in presence of a force →F=(αyˆi+2αxˆj)N, where x and y are in meter and α=−1Nm−1. The work done on the particle by this by this force will be Joule.
 View Solution
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionA force →F=(−yˆi+xˆj)N acts on a particle as it moves in an anticlockwise circular motion in x-y plane. The centre of the circle is at the origin. If the work done by the force is 32πJ in one complete revolution then asSigmaing x,y to be in meters, find the radius of the path.
View SolutionThe intensity of an electric field depends only on the coordinates x and y as follows,
E=a(xˆi+yˆj)x2+y2 where, a is constant and ˆi and ˆj are the unit vectors of the x and y axes. Find the charges within a sphere of radius R with the centre at the origin.View SolutionThe work done by a force F=(ˆi+2ˆj+3ˆk) N ,to displace a body from position A to position B is [The position vector of A is r1=(2ˆi+2ˆj+3ˆk)m The position vector of B is r2=(3ˆi+ˆj+5ˆk)m ]
View SolutionA body is displaced from prigin to (1m,1m) by force
F=(2yˆi+3x2ˆj) along two paths
(a) x=y (b) y=x2
Find the work done along both paths.View Solution


