A ray hits the y-axis making an angle θ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is μ=μ0(1−xd) for 0≤x≤d(1−1μ0) and μ=μ0 for x<0, where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
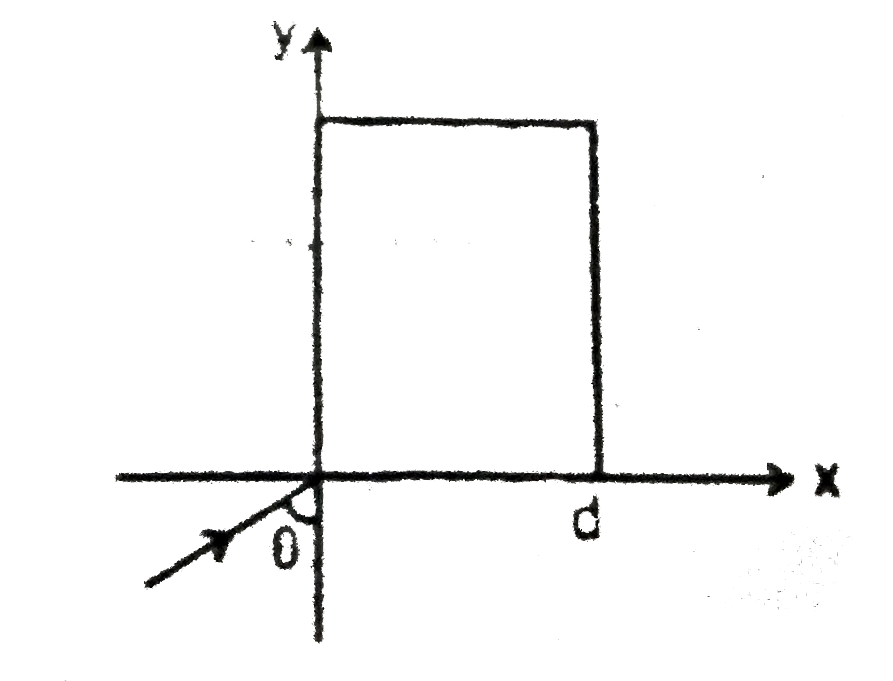
d(1−sinθ)
d(1−cosθ)
dsinθ
dcosθ
The correct Answer is:B
Snell's law =μ0sin(90∘−0)
=μ0(1−xd)sin90∘⇒(1−xd)=cosθ
⇒x=d(1−cosθ).
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.26
8 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.27
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.24
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Find the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
View SolutionA long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
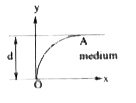
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
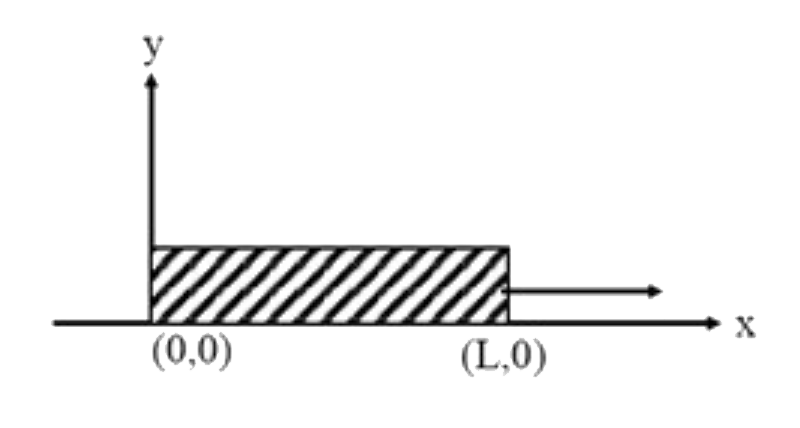
View SolutionA uniform rod of length L and mass M has been placed on a rough horizontal surface as shown in the figure. The rod is pulled by applying a horizontal force. The coefficient of friction μ between the surface and the rod is given by
μ={μ0x0≤x≤L0x>L, where μ0 is a positive constant. The heat generated due to friction as the rod moves by a distance L is
View SolutionA laser beam propagates through a spherically symmetric medium, as shown in the figure. The refractive index varies with the distance to the symmetry centre C by the law μ(r)=μ0rr0, where μ0=1, r0=3cm, r0≤r<∞. The beam's trajectory lies in the plane that includes C. At distance r1=8√2cm the beam makes an angle ϕ=30∘ with →r1 as shown in the figure. Find the minimum distance (in cm) the beam reach relative to the symmetry centre C.

View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA point source S is placed at the bottom of different layers as shown in the figure. The refractive index of bottom most layer is μ0. The refractive index of any other upper layer is μ(n)=μ0−μ04n−18 where n=1,2………….A ray of light with angle i slightly more than 30∘ starts from the source S. Total internal reflection takes place at the upper surface of a layer having n equal to

View SolutionA light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
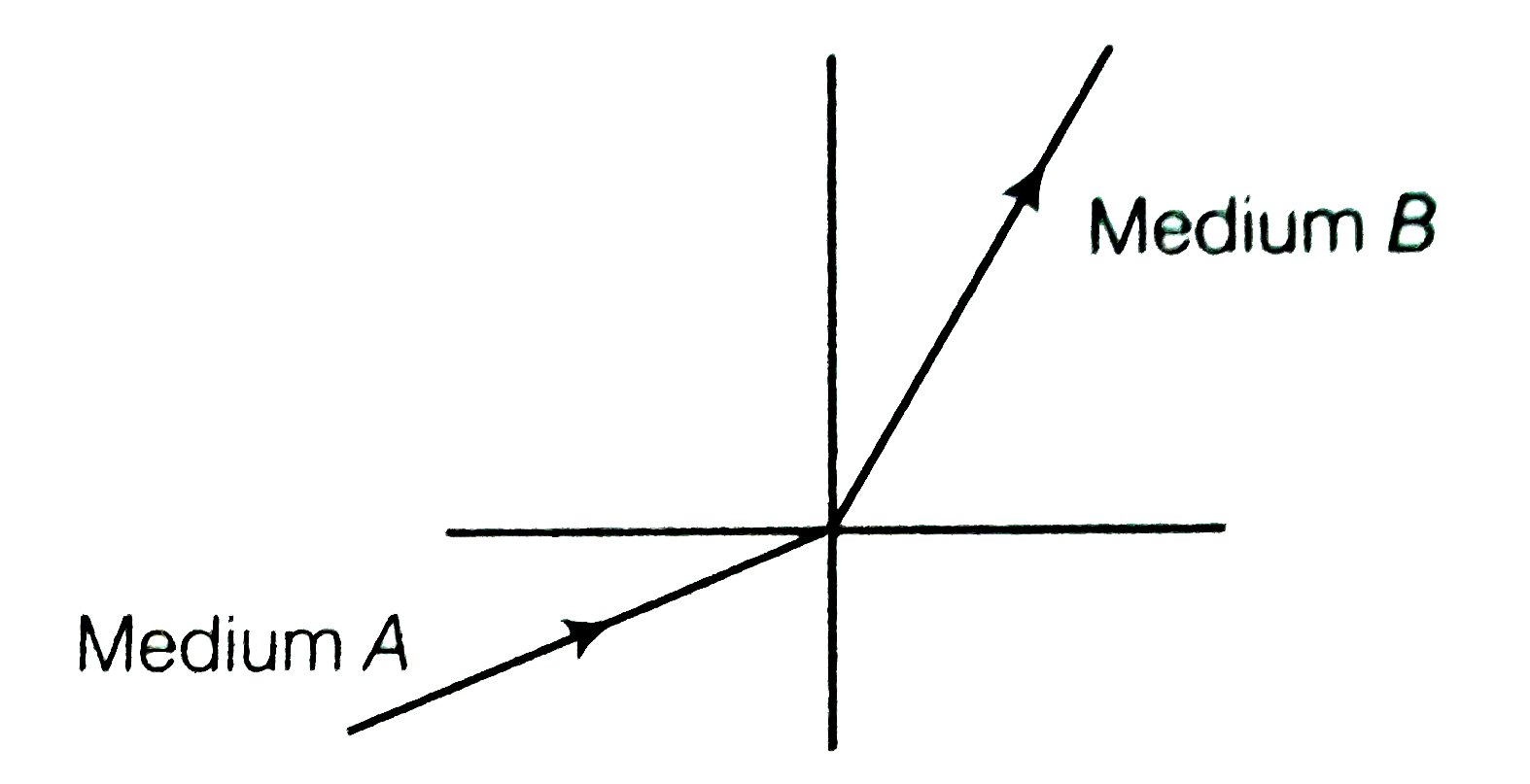
View SolutionFind the maximum angle of refraction when a light ray is refracted from glass (μ=1.50) to air.
View SolutionIn which of the following cases the friction force between A and B is maximum in all cases μ1=0.5,μ2=0.
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
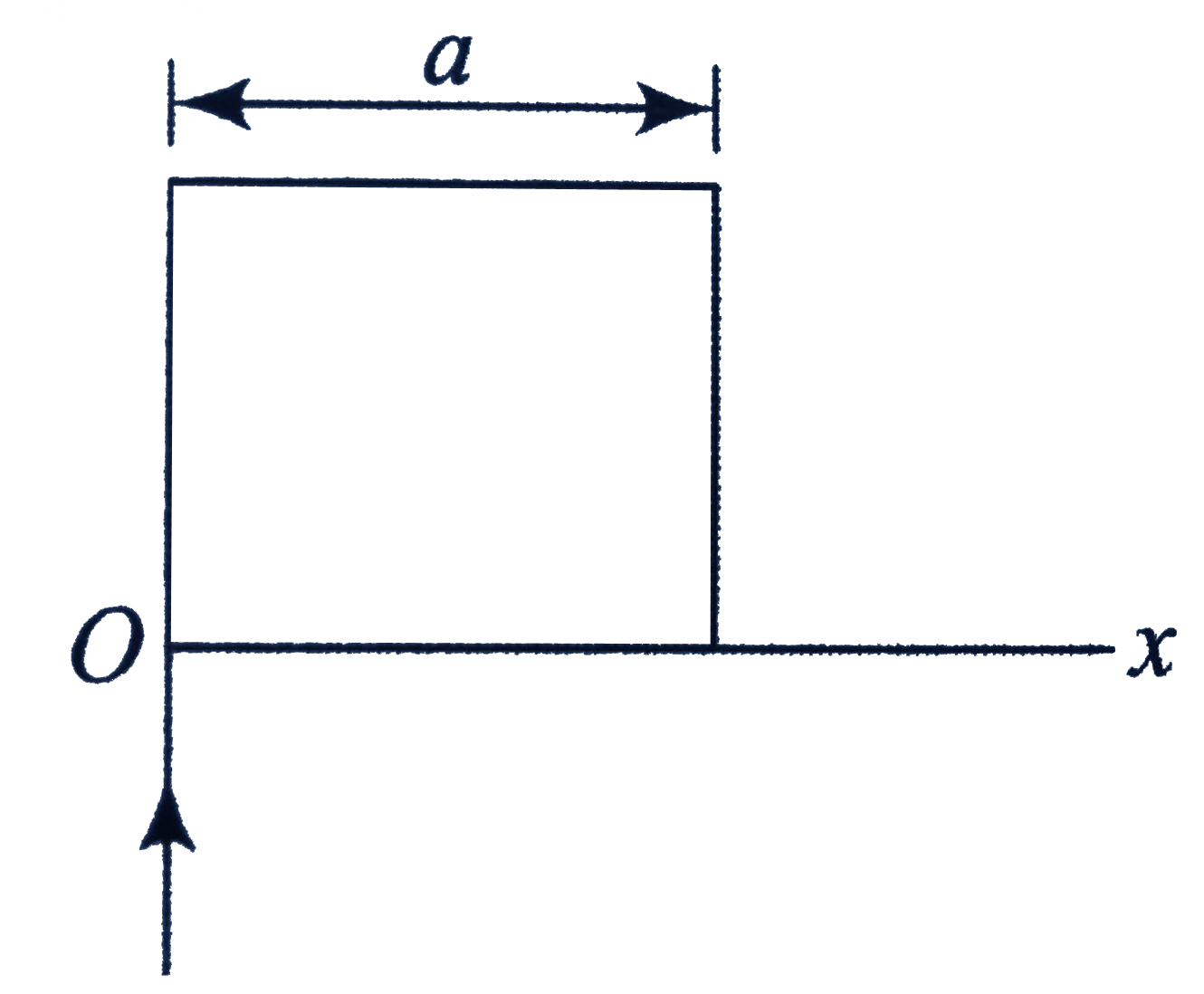
View Solution
