The intensity of an electric field depends only on the coordinates x and y as follows,
where, a is constant and and are the unit vectors of the x and y axes. Find the charges within a sphere of radius R with the centre at the origin.
The correct Answer is:A, D
At any point on the sphere a unit vector perpendicular to the sphere radially outwards is

as
Let us find the electric flux passing through a small area at point P on the sphere
here we not that is independent of the coordinates x,y, and z. Therefore,total flux passing through the sphere
From Gauss's law, hi=q_("in")/epsilon_0(4piaR)=q_("in")/epsilon_0:. q_("in")=4piepsilon_0aR
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The intensity of an electric field depends only on the co-ordinates x, y and z as follows:
→E=a(xˆi+yˆj+zˆk)(x2+y2+z2)3/2unit.
The electrostatic energy stored between two imaginary concentric spherical shells of radii R and 2R with centre at origin isView SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
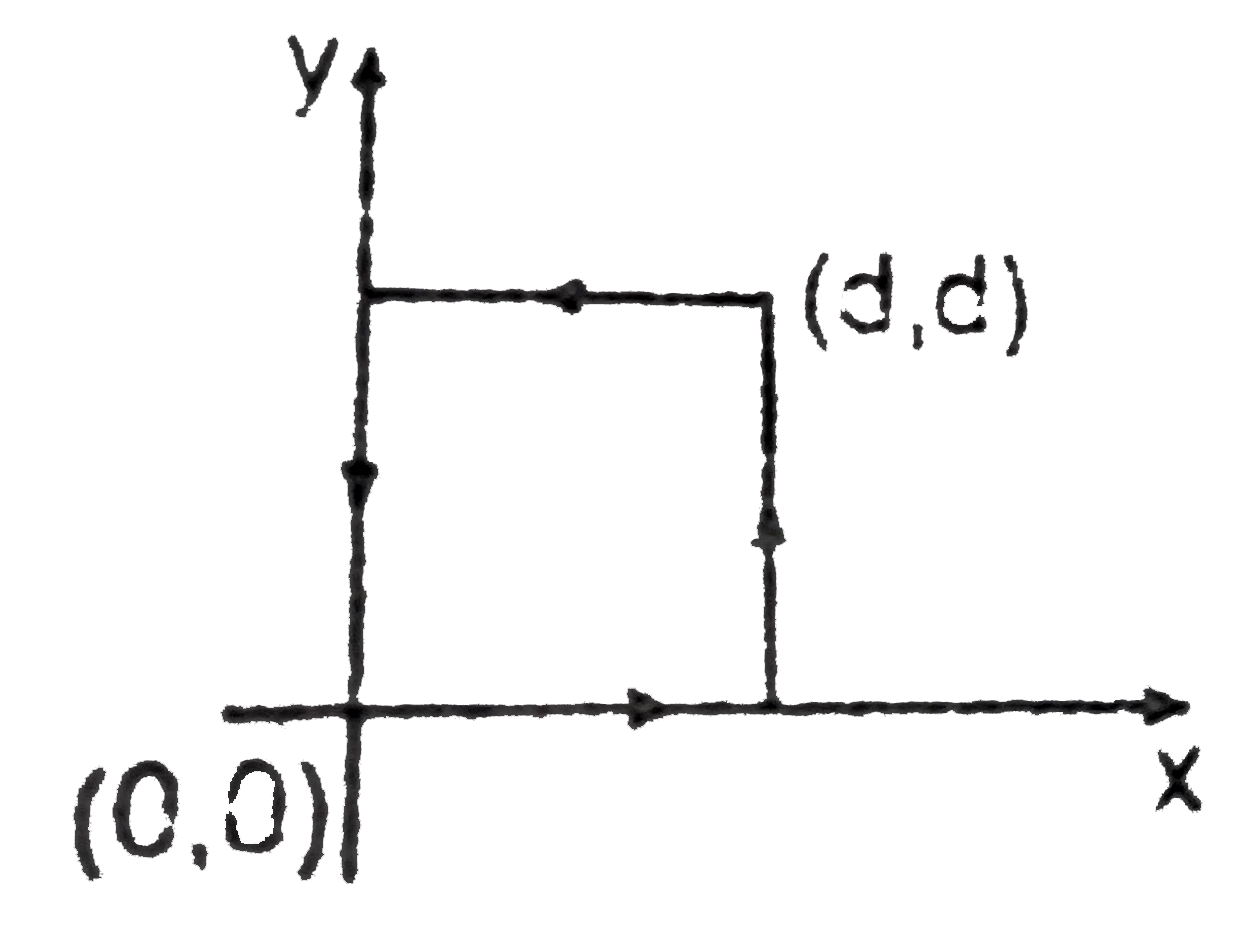 View Solution
View SolutionIf ˆi,ˆj and ˆk are unit vectors along X,Y & Z axis respectively, then what is the magnitude of ˆi+ˆj+ˆk
View SolutionA particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View SolutionIf ˆi and ˆj are unit vectors along X-and Y-axis respectively, then what is the magnitude and direction of ˆi+ˆj and ˆi−ˆj ?
View SolutionIf ˆi,ˆj and ˆk are unit vectors along X,Y & Z axis respectively, then tick the wrong statement:
View SolutionThe electric field strength depends only on the x, y, and z coordinates according to the law E=a(xˆi+yˆj+zˆk)(x2+y2+z2)3/2, where a=280Nm2C−1 is a constant. If the potential difference between (3,2,6) and (0,3,4) is x2. What is the value of x.
View SolutionDetermine the electric field strength vector if the potential of this field depends on x, coordinates as
(a) V=a(x2—y2) (b) V=axy
where, a is a constant.View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
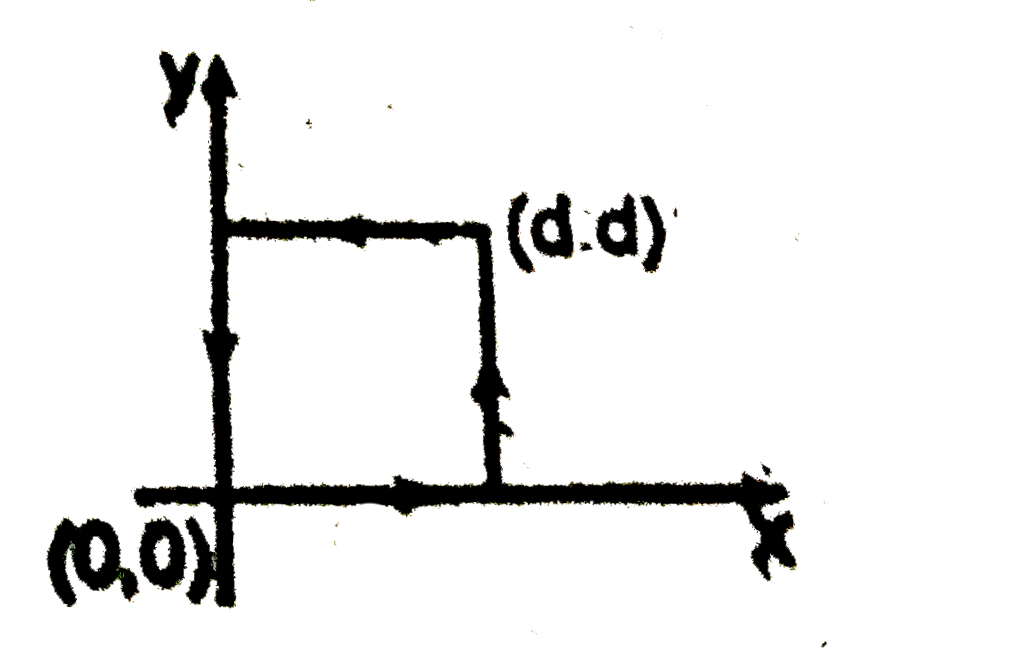 View Solution
View SolutionA system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
View Solution


