A force →F=(−yˆi+xˆj)N acts on a particle as it moves in an anticlockwise circular motion in x-y plane. The centre of the circle is at the origin. If the work done by the force is 32πJ in one complete revolution then asSigmaing x,y to be in meters, find the radius of the path.
To solve the problem, we will follow these steps:
Step 1: Understand the Given Force
The force acting on the particle is given as:
→F=(−y^i+x^j)N
This means that the force has components in the negative y-direction and the positive x-direction.
Step 2: Identify the Motion of the Particle
The particle is moving in an anticlockwise circular motion in the x-y plane, with the center of the circle at the origin (0,0). The position vector of the particle can be expressed as:
→R=x^i+y^j
Since the motion is circular, we can relate the position to the radius R of the circle.
Step 3: Calculate the Torque
The torque τ acting on the particle is given by the cross product of the position vector →R and the force →F:
τ=→R×→F
Since the force is perpendicular to the radius in circular motion, the magnitude of the torque can be simplified to:
|τ|=R⋅|→F|
Where R is the radius of the circle.
Step 4: Work Done by the Force
The work done W by the torque over one complete revolution (from 0 to 2π) can be expressed as:
W=∫2π0τdθ
Given that the torque is constant, this simplifies to:
W=τ⋅Δθ=τ⋅(2π)
Step 5: Relate Work Done to Torque
From the previous steps, we know:
W=R2⋅2π
We are given that the work done is 32πJ. Therefore, we can set up the equation:
R2⋅2π=32π
Step 6: Solve for Radius R
We can simplify the equation by dividing both sides by 2π:
R2=32π2π=16
Taking the square root of both sides gives:
R=√16=4meters
Final Answer
The radius of the path is R=4meters.
---
The force acting on the particle is given as:
→F=(−y^i+x^j)N
This means that the force has components in the negative y-direction and the positive x-direction.
The particle is moving in an anticlockwise circular motion in the x-y plane, with the center of the circle at the origin (0,0). The position vector of the particle can be expressed as:
→R=x^i+y^j
Since the motion is circular, we can relate the position to the radius R of the circle.
The torque τ acting on the particle is given by the cross product of the position vector →R and the force →F:
τ=→R×→F
Since the force is perpendicular to the radius in circular motion, the magnitude of the torque can be simplified to:
|τ|=R⋅|→F|
Where R is the radius of the circle.
The work done W by the torque over one complete revolution (from 0 to 2π) can be expressed as:
W=∫2π0τdθ
Given that the torque is constant, this simplifies to:
W=τ⋅Δθ=τ⋅(2π)
From the previous steps, we know:
W=R2⋅2π
We are given that the work done is 32πJ. Therefore, we can set up the equation:
R2⋅2π=32π
We can simplify the equation by dividing both sides by 2π:
R2=32π2π=16
Taking the square root of both sides gives:
R=√16=4meters
The radius of the path is R=4meters.
Similar Questions
A force →F=b−yˆi+xˆjx2+y2N( b is a constant ) acts on a particle as it undergoes counterclockwise circular motion in a circle :x2+y2=16. The work done by the force when the particle undergoes one complete revolution is ( x,y are in m )
View SolutionIf →E=2yˆi+2xˆj, then find V(x,y,z)
View SolutionThe position of a particle at time moving in x−y plane is given by →r=ˆi+2ˆjcosωt. Then, the motikon of the paricle is :
View SolutionA uniform force of (3ˆi+ˆj) newton acts on a particle of mass 2kg. Hence the particle is displaced from position (2ˆi+ˆk) meter to position (4ˆi+3ˆj−ˆk) meter. The work done by the force on the particle is :
View SolutionA force →F=(5ˆi+3ˆj)N is applied over a particle which displaces it from its origin to the point →r=(2ˆi−1ˆj) meter. The work done on the particle is :
View SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
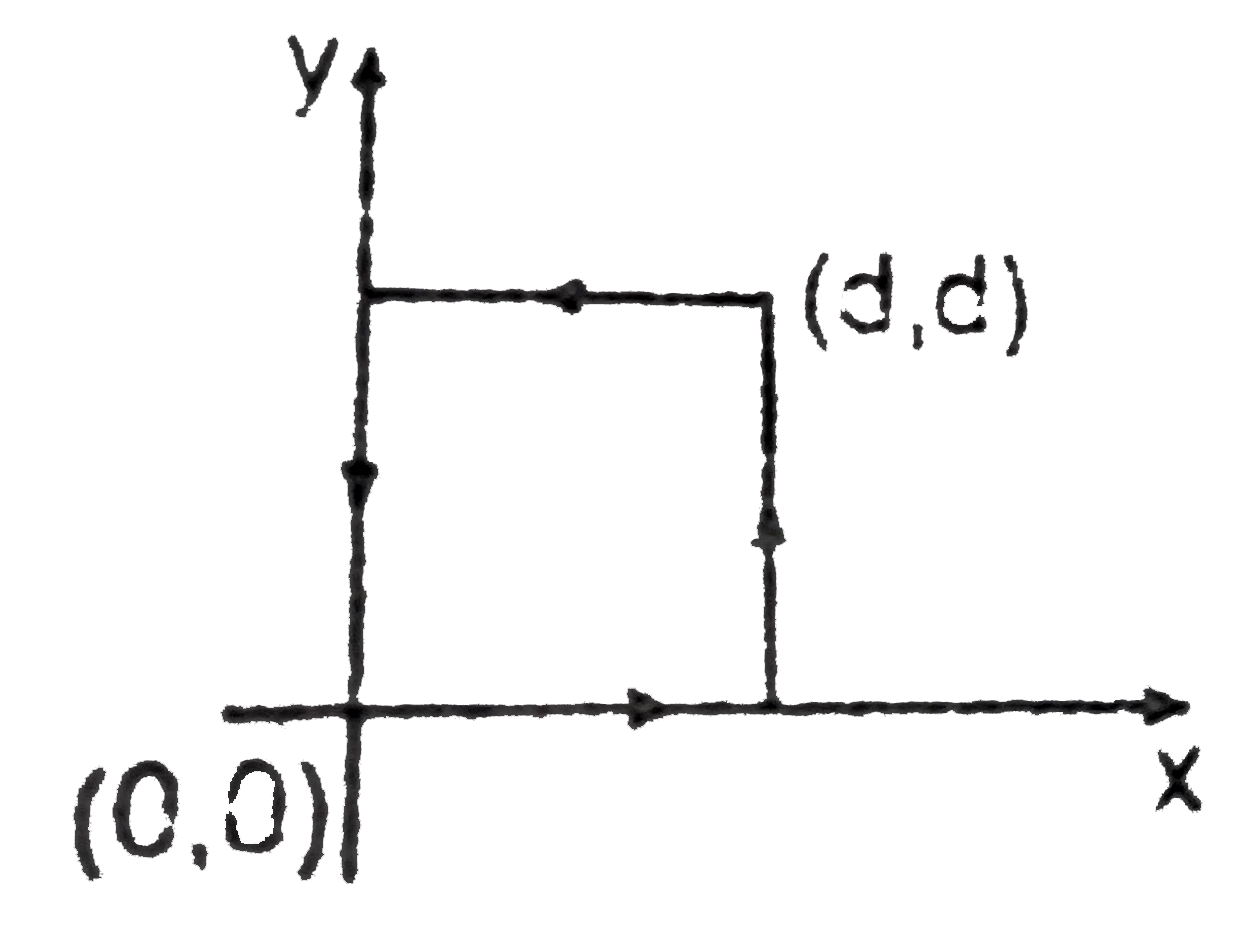
View SolutionA force →F=2ˆi−3ˆj+7ˆk(N) acts on a particle which undergoes a displacement →r=7ˆj+3ˆj−2ˆk(m). Calculate the work done by the force.
View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
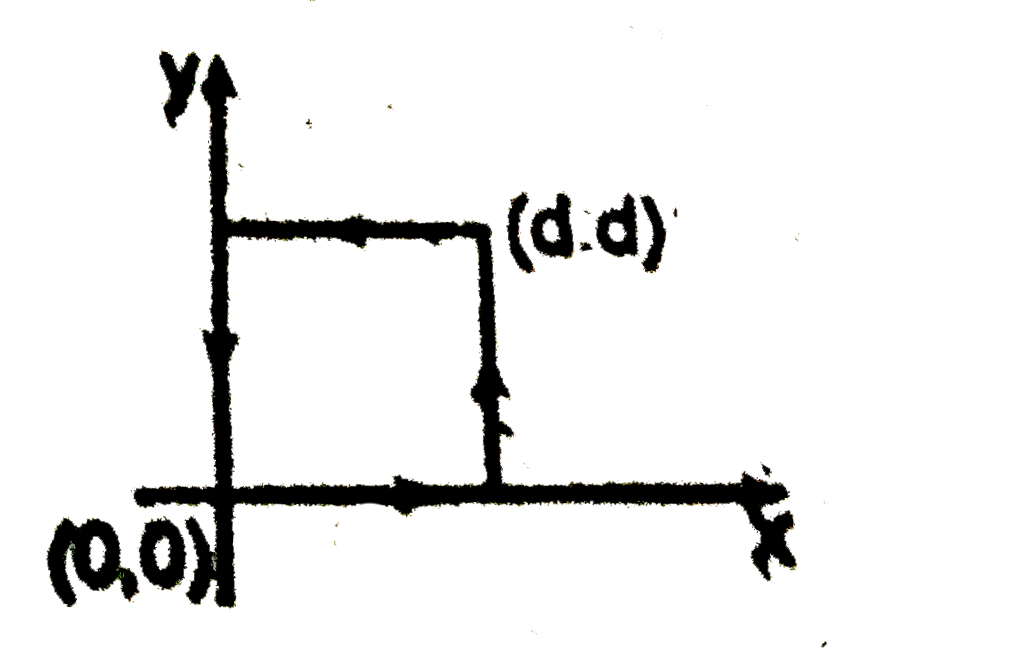
View SolutionIf →E=2x2ˆi−3y2ˆj, then V (x, y, z)
View SolutionA force bar F = (3hat i-4 hat j +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
View Solution
