A particle is moved along the different paths as shown in the figure . Path is a parabola , . Find the work done by a forc on the particle along these paths. Is this force a conservative force ?
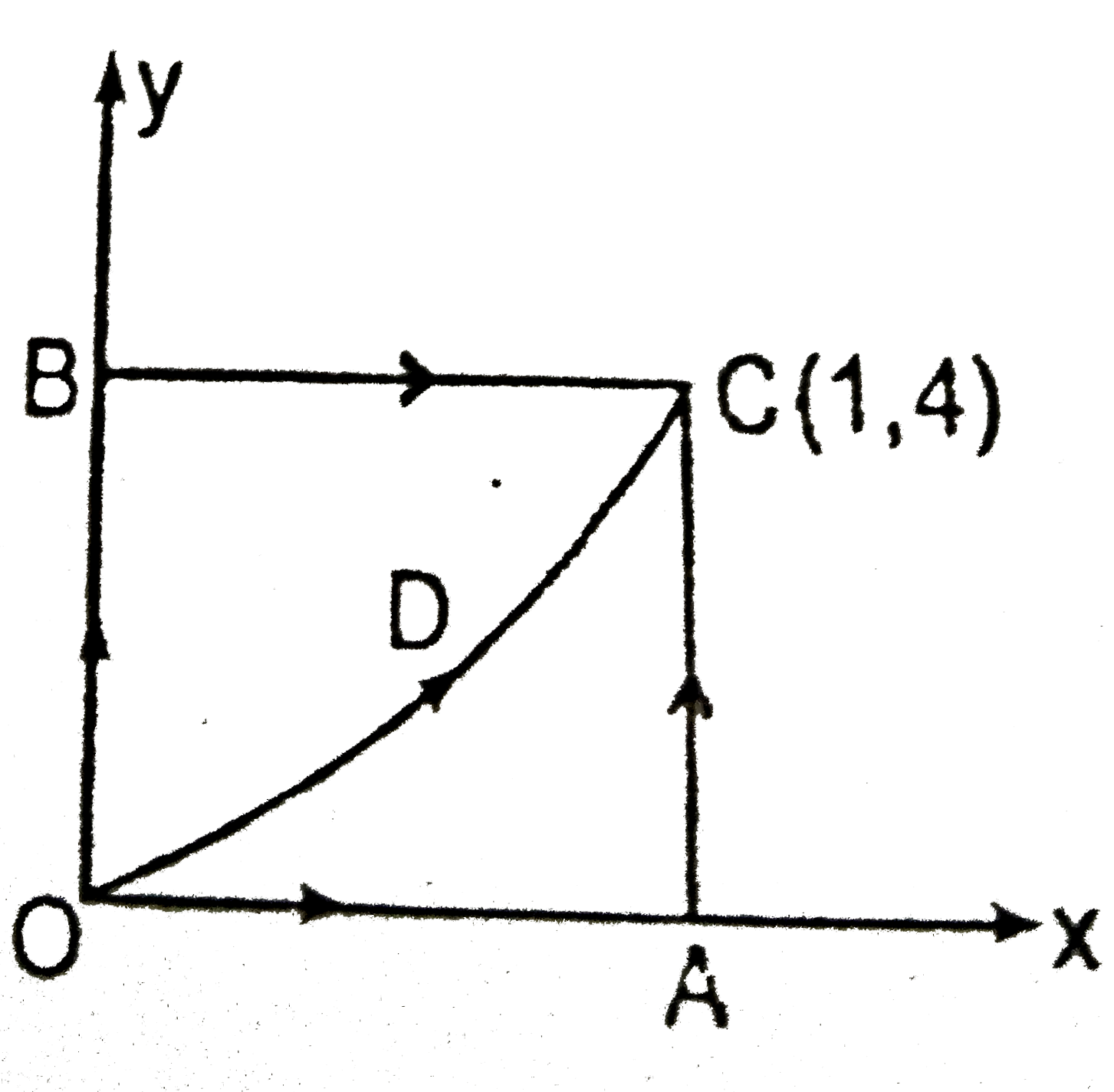
The correct Answer is:
ON path
and on path
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 40
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 41
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 38
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A particle is moved foom the orgin A, back to the origin, along the path ABCDEFA as shown in figure

(A) Find the work done by the force →F=yˆi+zˆj+xˆk acting on the particle, in the round trip?
(B) Is the force given in part (A) conservative?
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View Solution
Knowledge Check
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
A particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

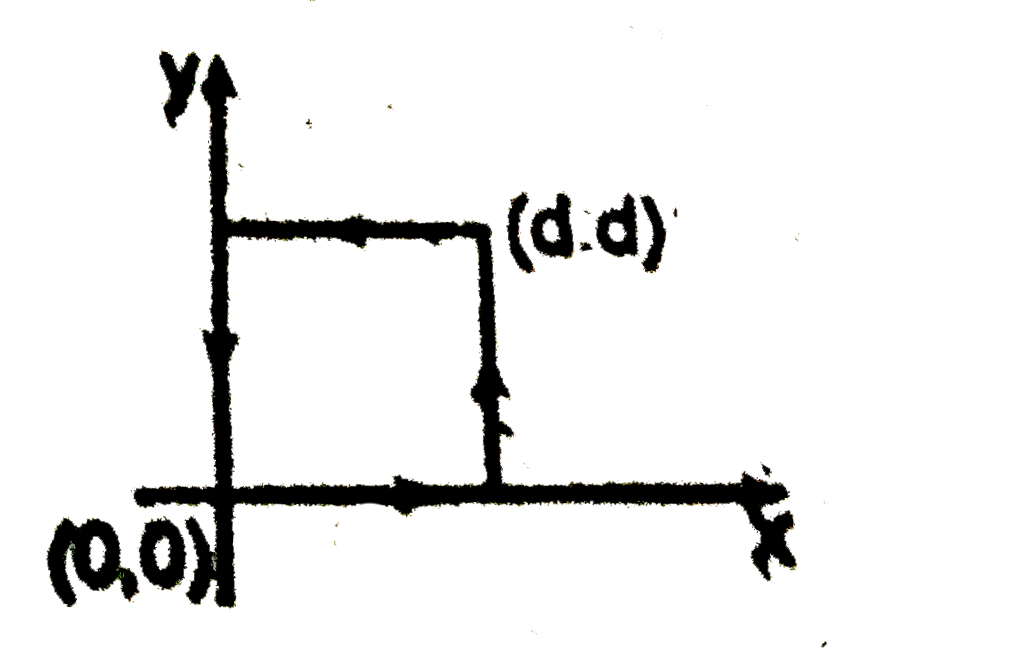
View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
View SolutionShown that work done by a conservative force on a particle moving between two points is path independent.
View SolutionA particle is moved inx−y plane form (a,0) to (0,a) along circular arc having centre at origin. Work done by a force −ky(x2+y2)32ˆi+kx(x2+y2)32ˆj on the particle during this motion will be
View SolutionA particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
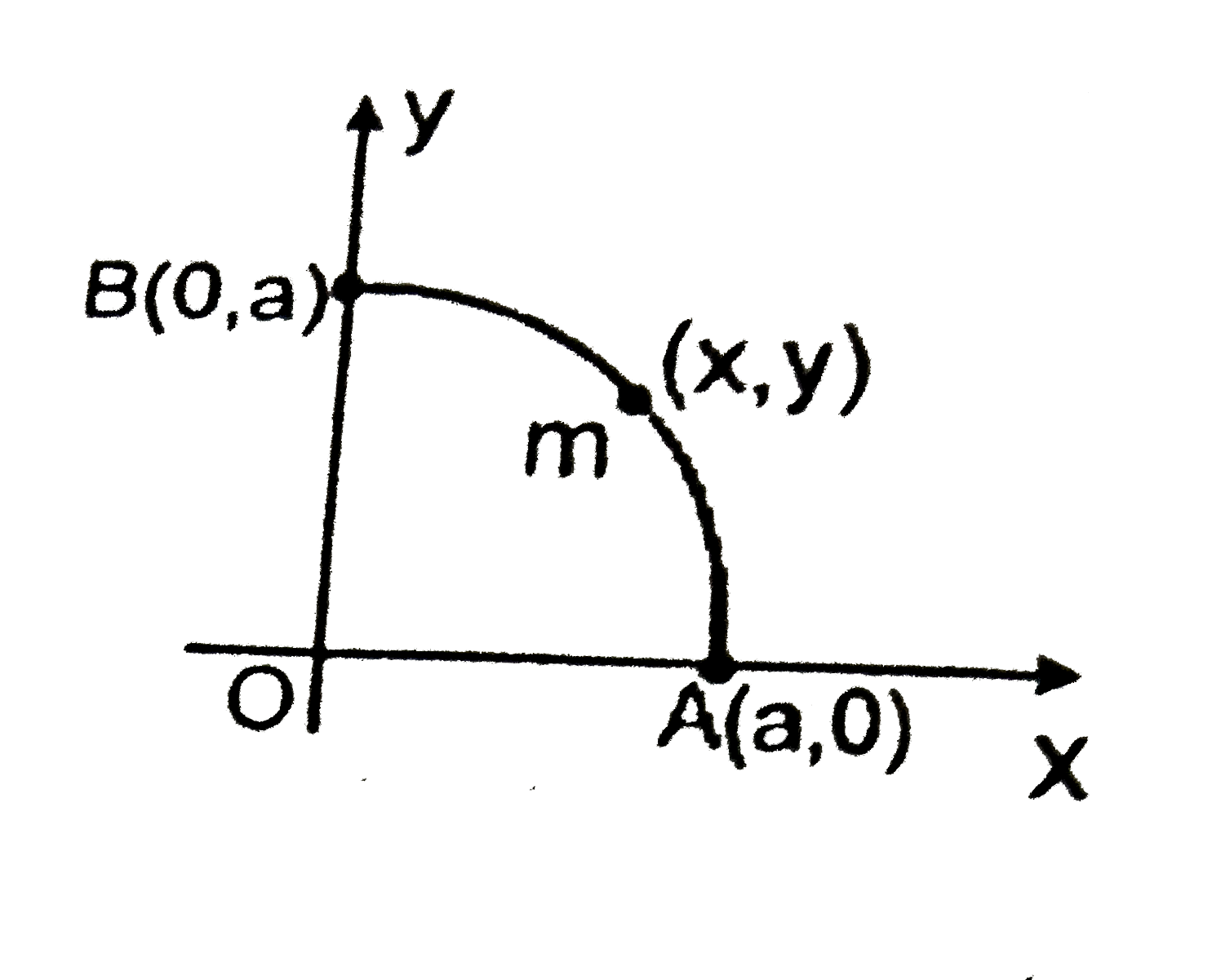
View SolutionA particle is moving with a constant speed along a straight line path. A force is not required to
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View Solution