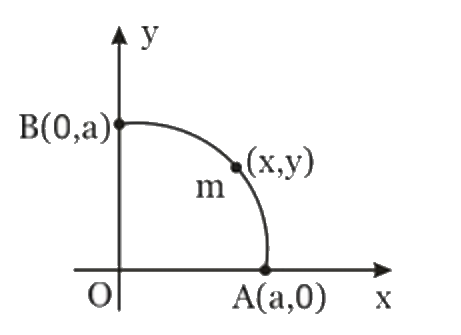
A particle of mass m moves along the quarter section of the circular parth whose centre is at the origin. The radius of the circular path is a. A force →F=yˆi−xˆj N acts on the particle, where x, y denote the coordinates of the position of the particle. Calculate the work done by this force in taking the particle from point A(a, 0) to point B(0, a) along the circular path.
The correct Answer is:−πa22
Work done by force F,
w=∫→F.d→r=∫(yˆi−xˆj).(dxˆi+dyˆj)
∴x2+y2=a2∴xdx+ydy=0
⇒W=∫(y(−ydyx)−xdy)
−∫(x2+y2)xdy
=−∫a0a2√a2−y2dy=−πa22
Aternate Method
It can be observed that the force is tangent to the curve at each point and the magnitude is constant. The direction of force is opposite to the direction of motion of the particle.
∴ work done =(force) × (distance)
=−√x2+y2πa2=−a×πa2=−πa22J
Ans. w=−πa22J
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 40
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 41
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 38
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
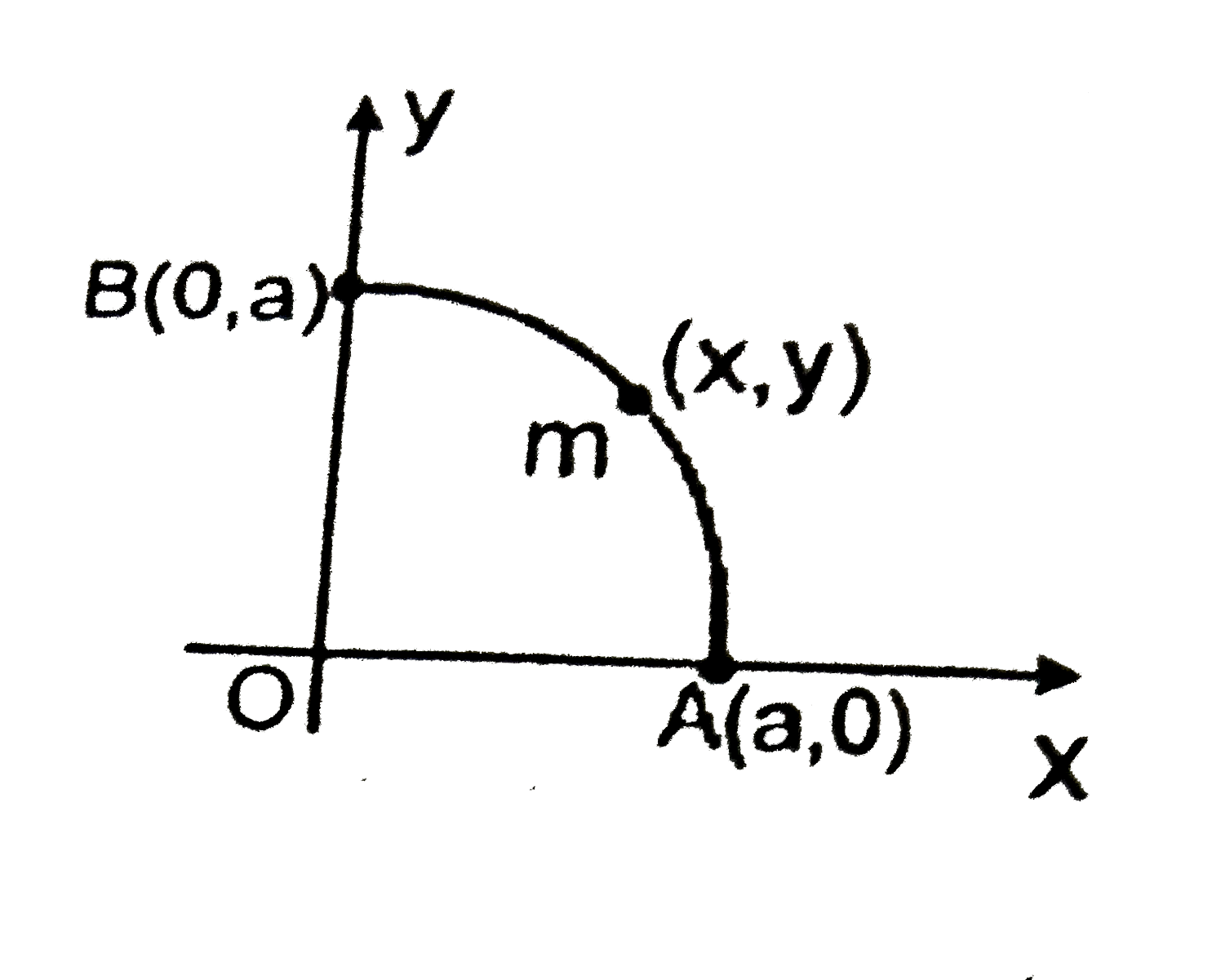
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View Solution
Knowledge Check
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 JA particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
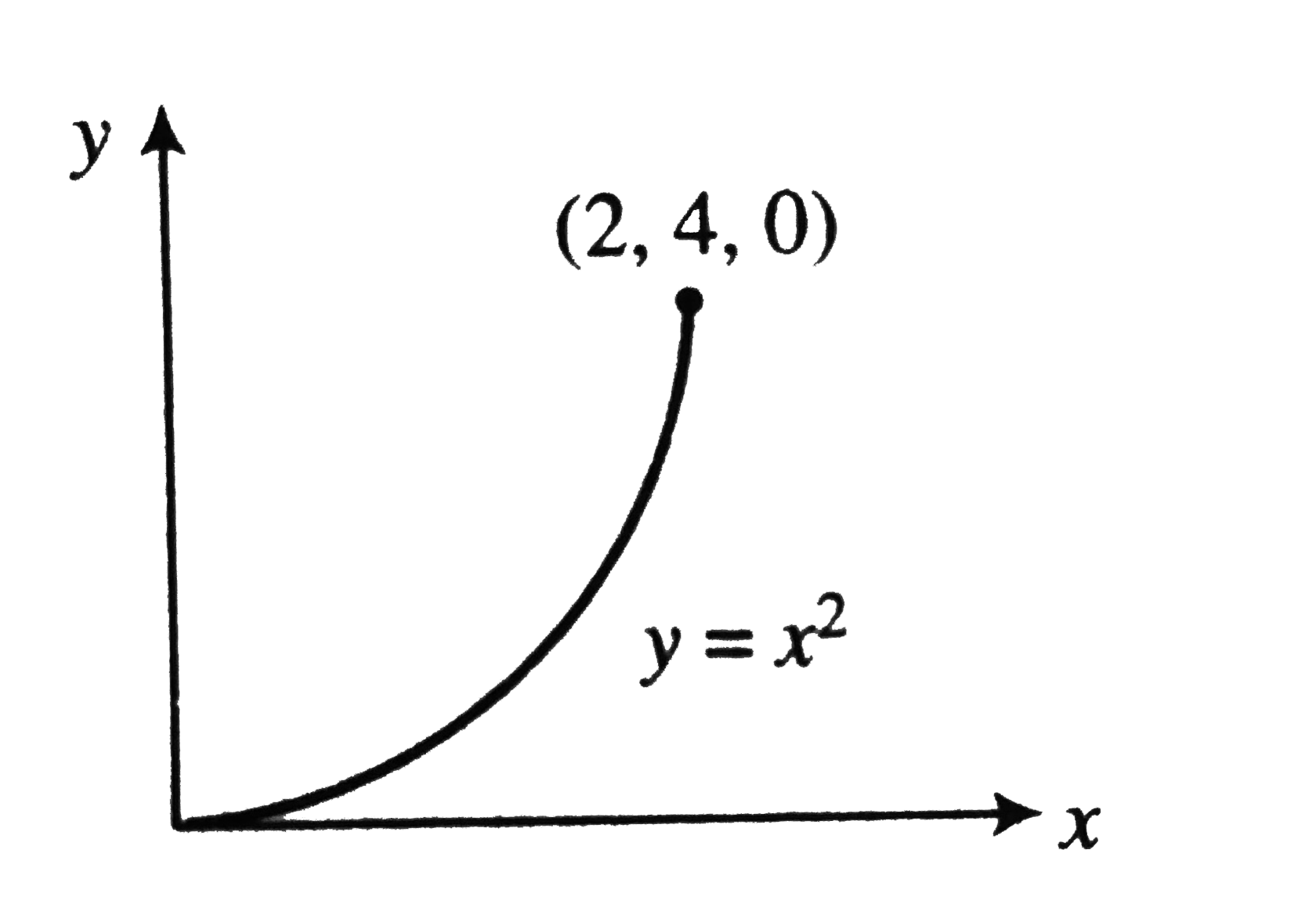
A force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA force →F=(2xˆi+3ˆj+3z2ˆk) is acting on the particle of mass 2kg which is displaces from point A(2,3,0) to point B(3,2,1). the work done by the force on the particle will be
View SolutionForce on a particle varies with position (x) of particle as shown, calculate work done by force from x=0 to x=30 m.

View SolutionA force (F) acting on a particle varies work done by a particle varies with the with the position x as shown in figure
 .
.
Find the work done by by force in displacing the particle from .
(a) x=−2m to x=0
(b) x=0 to x=2m..
View Solution