A charged capacitor is discharged through a resistance. The time constant of the circuit is η. Then the value of time constant for the power dissipated through the resistance will be
η
2η
η2
zero
The correct Answer is:C
To solve the problem of finding the time constant for the power dissipated through a resistance when a charged capacitor is discharged, we can follow these steps:
1. Understanding the Circuit:
A capacitor discharges through a resistor. The time constant (τ) of the RC circuit is defined as τ = R * C, where R is the resistance and C is the capacitance.
2. Current Equation:
The current (I) flowing through the circuit at any time t during the discharge can be expressed as:
I(t)=I0e−t/η
where I0 is the initial current and η is the time constant.
3. Power Dissipation:
The power (P) dissipated in the resistor can be calculated using the formula:
P=I2R
Substituting the expression for current, we get:
P(t)=(I0e−t/η)2R
This simplifies to:
P(t)=I20Re−2t/η
4. Identifying the New Time Constant:
The expression for power can be rewritten as:
P(t)=(I20R)e−2t/η
From this equation, we can see that the power dissipated also follows an exponential decay, but with a new time constant.
5. Finding the New Time Constant:
The new time constant for the power dissipation can be identified from the exponent of the exponential term. In this case, the time constant for power is:
New Time Constant=η2
Final Answer:
The time constant for the power dissipated through the resistance is η2.
---
A capacitor discharges through a resistor. The time constant (τ) of the RC circuit is defined as τ = R * C, where R is the resistance and C is the capacitance.
The current (I) flowing through the circuit at any time t during the discharge can be expressed as:
I(t)=I0e−t/η
where I0 is the initial current and η is the time constant.
The power (P) dissipated in the resistor can be calculated using the formula:
P=I2R
Substituting the expression for current, we get:
P(t)=(I0e−t/η)2R
This simplifies to:
P(t)=I20Re−2t/η
The expression for power can be rewritten as:
P(t)=(I20R)e−2t/η
From this equation, we can see that the power dissipated also follows an exponential decay, but with a new time constant.
The new time constant for the power dissipation can be identified from the exponent of the exponential term. In this case, the time constant for power is:
New Time Constant=η2
The time constant for the power dissipated through the resistance is η2.
Topper's Solved these Questions
- CAPACITORSBook:DC PANDEY ENGLISHChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
- CAPACITORSBook:DC PANDEY ENGLISHChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
- ATOMSBook:DC PANDEY ENGLISHChapter:ATOMSExercise:MEDICAL ENTRANCES GALLERY
Explore 42 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
Similar Questions
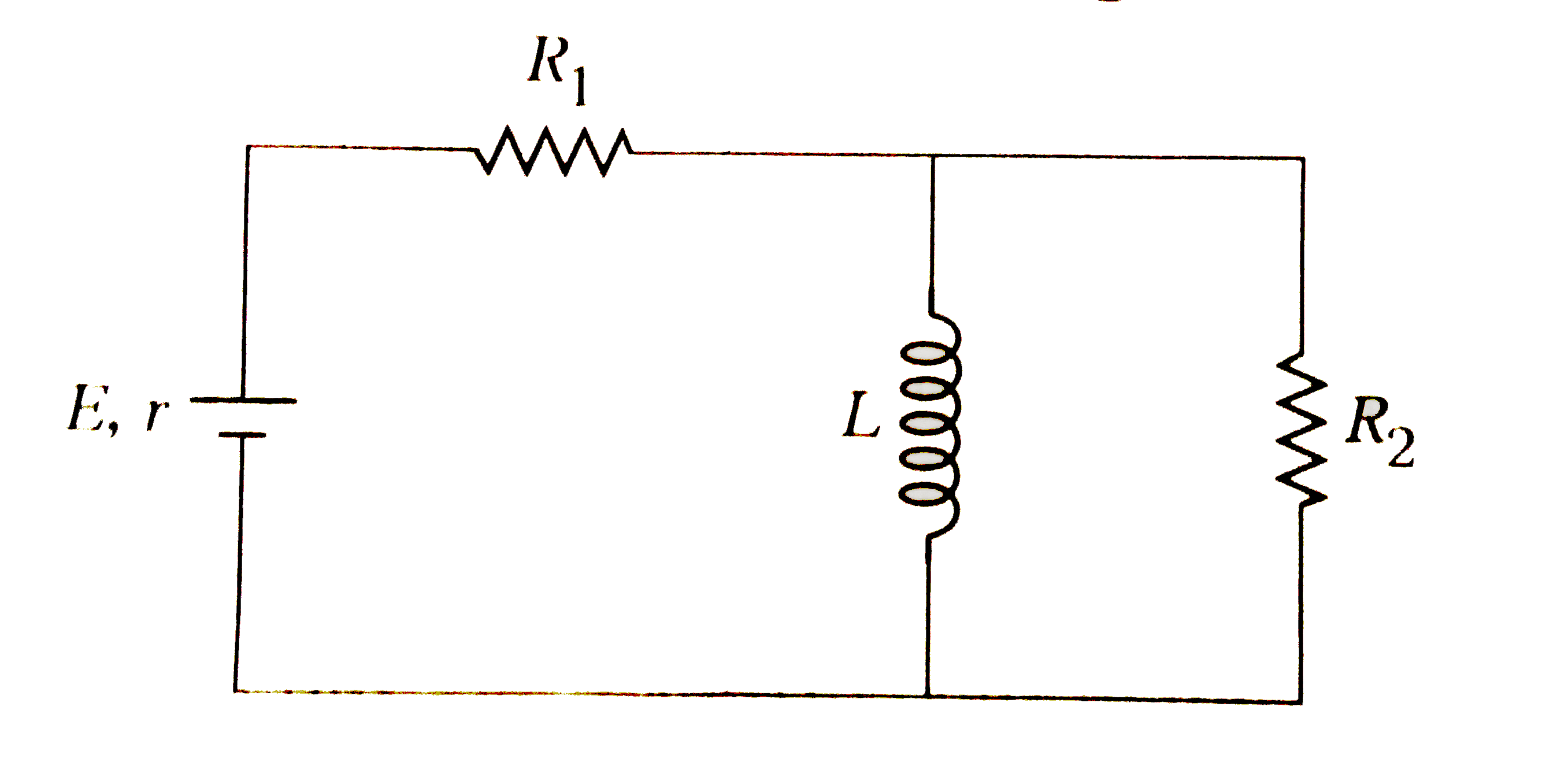
The value of time constant for the given circuit is
View SolutionA capacitor discharges through a resistance. The stored energy U0 in one capacitive time constant falls to
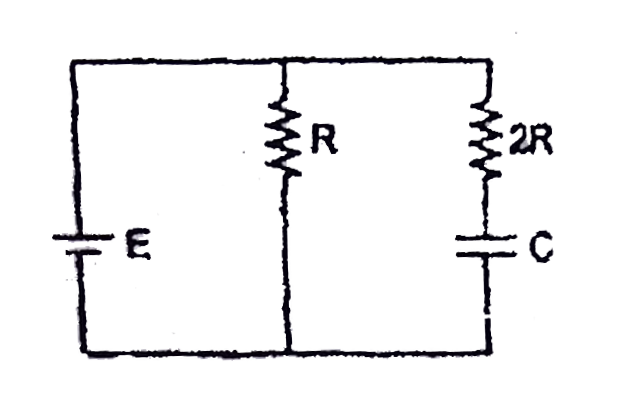
View SolutionThe time constant of charging of the circuit shown in figure is
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionA charged capacitor C1 is discharged through a resistance R by putting switch S in position 1 of the circuit as shown in fig.5.201. When the discharge current reduces to i0, the switch is suddenly shifted to position 2. Calculate the amount of heat liberated in resistor R starting form this instant. Also calculate current I through the circuit as a function of time.

View SolutionA charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ.Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
View SolutionA capacitor of capacitance 5μF is charged to a potential difference 200 V and then allowed to dischage through a resistance 1kΩ. The cahrge on the capacitor at the instant the current through the resistance is 100 Ma, is (in μC):
View SolutionA capacitor of capacitance C is allowed to discharge through a resistance R. The net charge flown through resistance during one time constant is (I0 is the maximum current)
View SolutionThe time constant T for the shown circuit containing resistance and capacitor, is
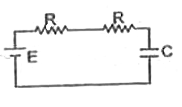
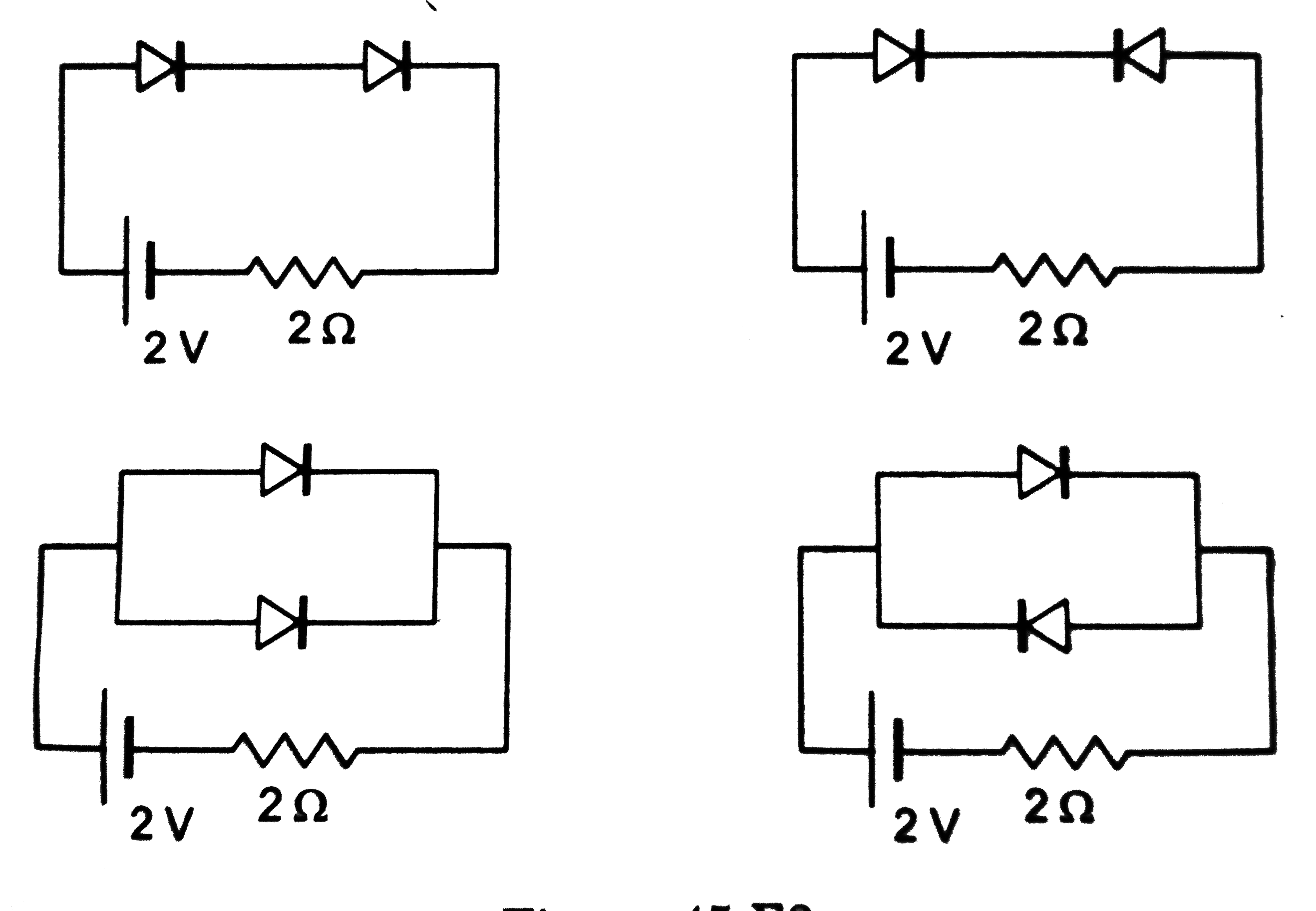
View SolutionFind the current through the resistance in the circuits shown in figure
View Solution

