A charged capacitor C1 is discharged through a resistance R by putting switch S in position 1 of the circuit as shown in fig.5.201. When the discharge current reduces to i0, the switch is suddenly shifted to position 2. Calculate the amount of heat liberated in resistor R starting form this instant. Also calculate current I through the circuit as a function of time.

The correct Answer is:A, B, C
Capacitor C1 will discharge according to the equation
q=q0e−tτC …………..i
Here, τC=C1R
and discharging current.
i=−dqdt=q0τC.e−tτC=⎛⎜⎝q0e−tτCC1R⎞⎟⎠……….ii
At the given instant i=i0
Therefore from eqn ii
q0e−tτC=i0C1R at this instant.
or charge C1 at this instant will be
q=(i0C1R) [From eqn ii]
Now this charge q will later on distribute in C1 and C2 .
∴Ui=q22C1+C2=Uf
∴ Heat genetrated in resistance.
H=Ui=Uf
Susbtituging values of q:Ui and Uf we get
H=(I0R)2C1C2(2(C1+C2))
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionIn the circuit shown, the switch S is shifted to position 2 from position 1 at t=0, having been in position 1 for a long time.Find the current in the circuit as a function of time.
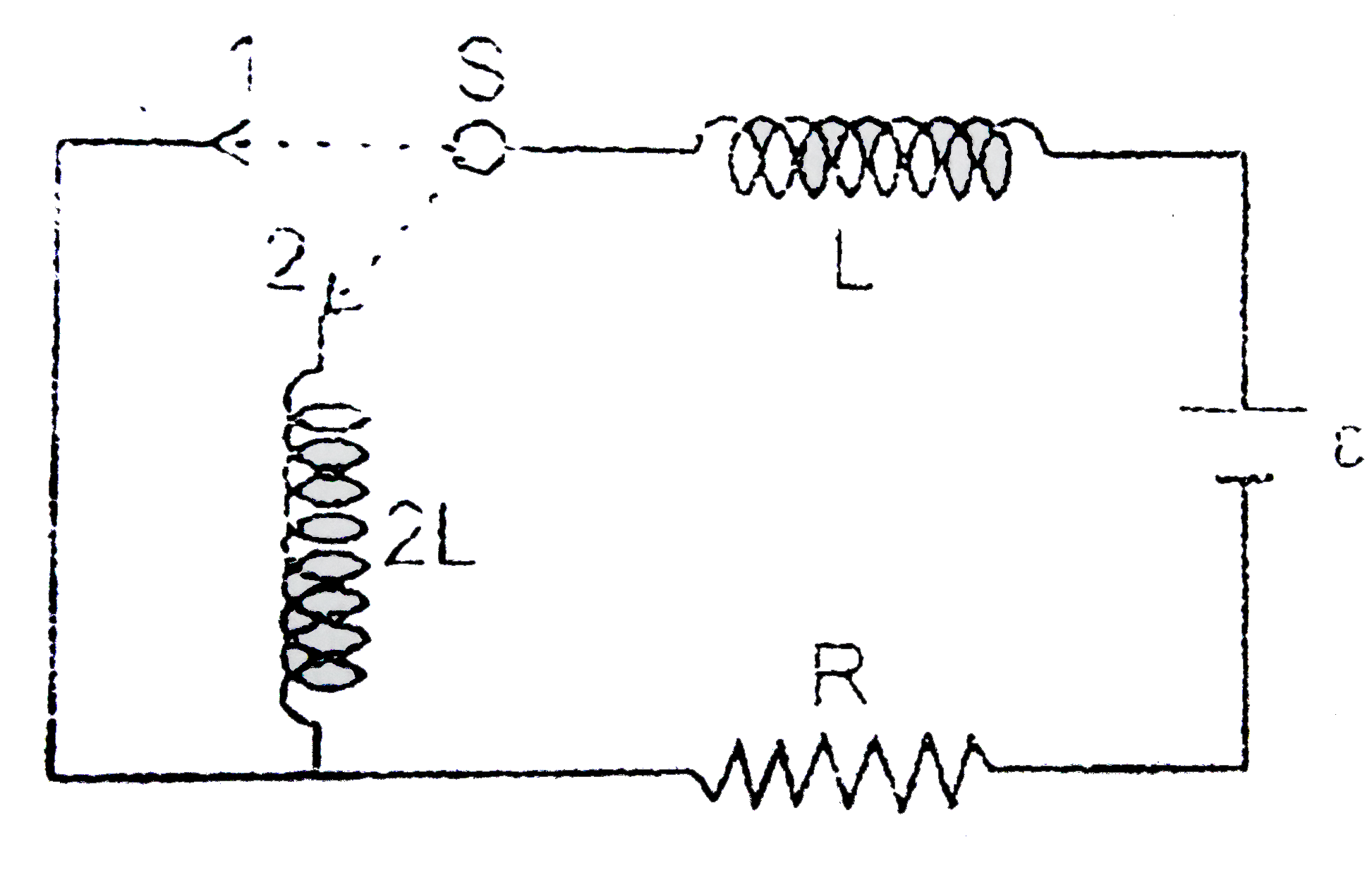
View SolutionIn the circuit shown, the switch S is shifted to position 2 from position 1 at t=0, having been in position 1 for a long time.Find the current in the circuit as a function of time.

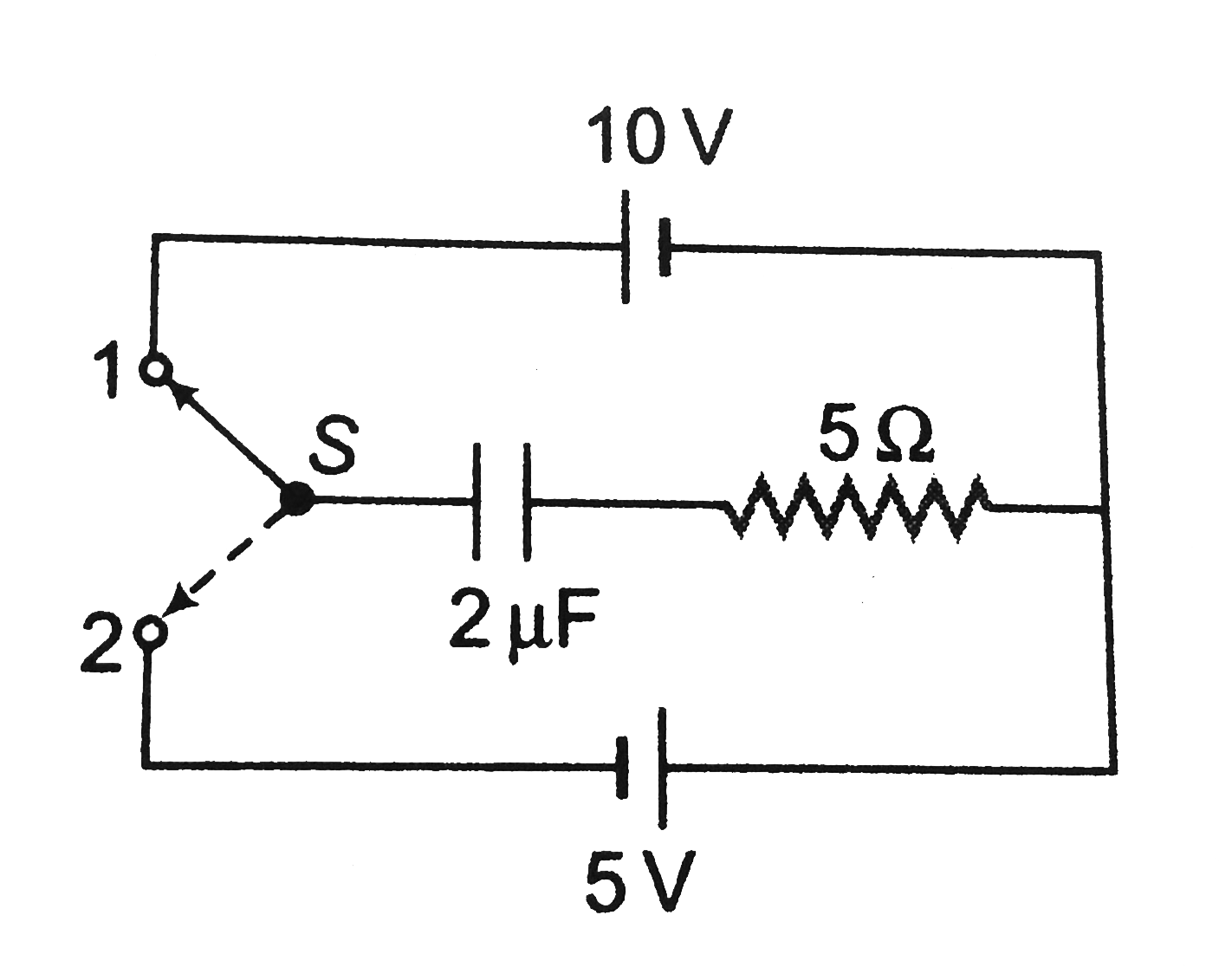
View SolutionIn the circuit shown in figure switch S is thrown to position 1 at t=0. when the current in the resistort is 1A, it is shifted to position 2. the total heat generated in the circuit after shifting to position 2 is
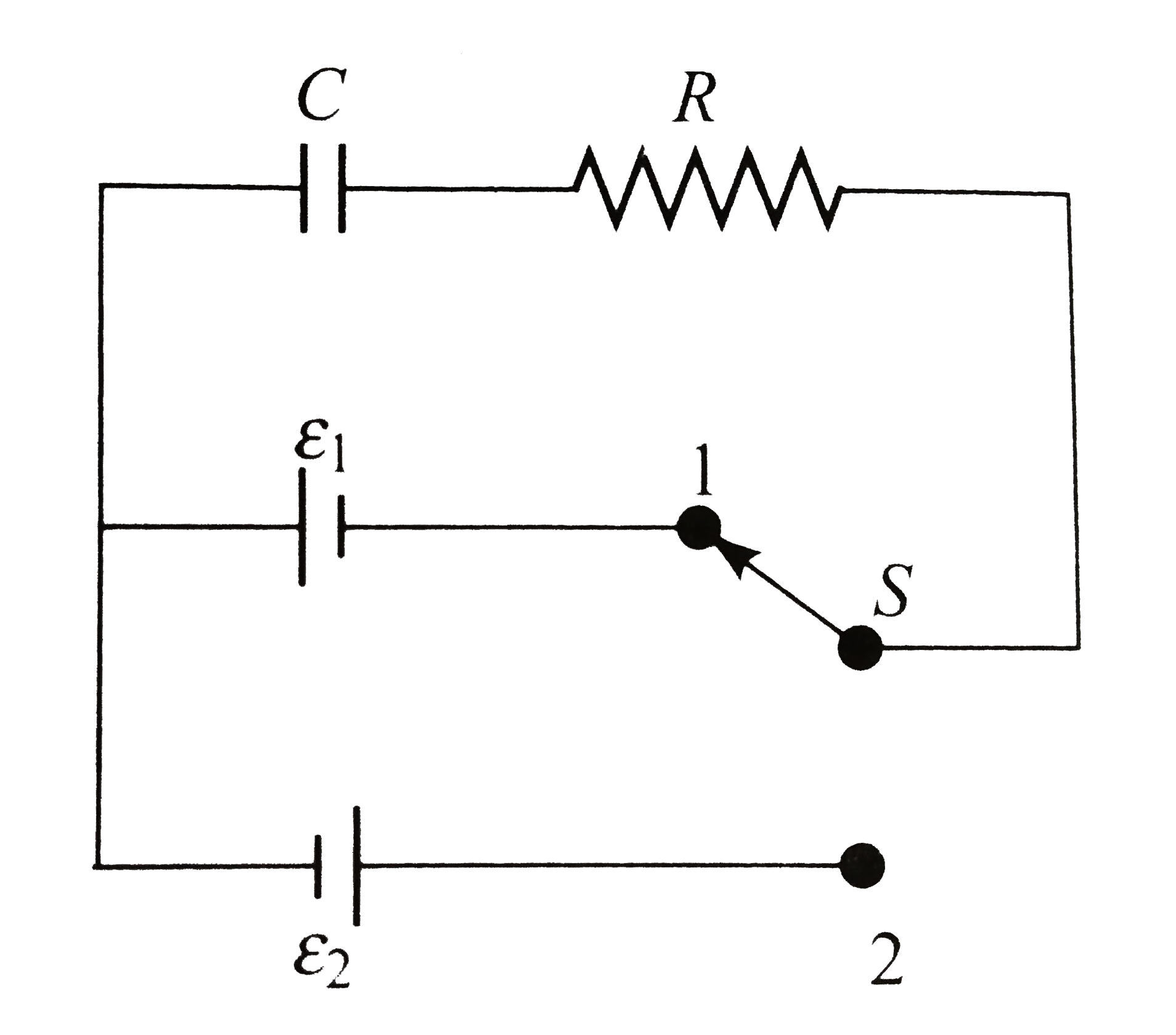
View SolutionInitially, switch S is connected to position 1 for a long time . The net amount of heat generated in the circuit after it is shifted to position 2 is .
View SolutionIn the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are

View SolutionThe capacitor C shown in the figure is in steady state condition when switch is shifted from position 1 to position 2.The heat liberated in the process is
_PHY_E05_272_Q01.png)
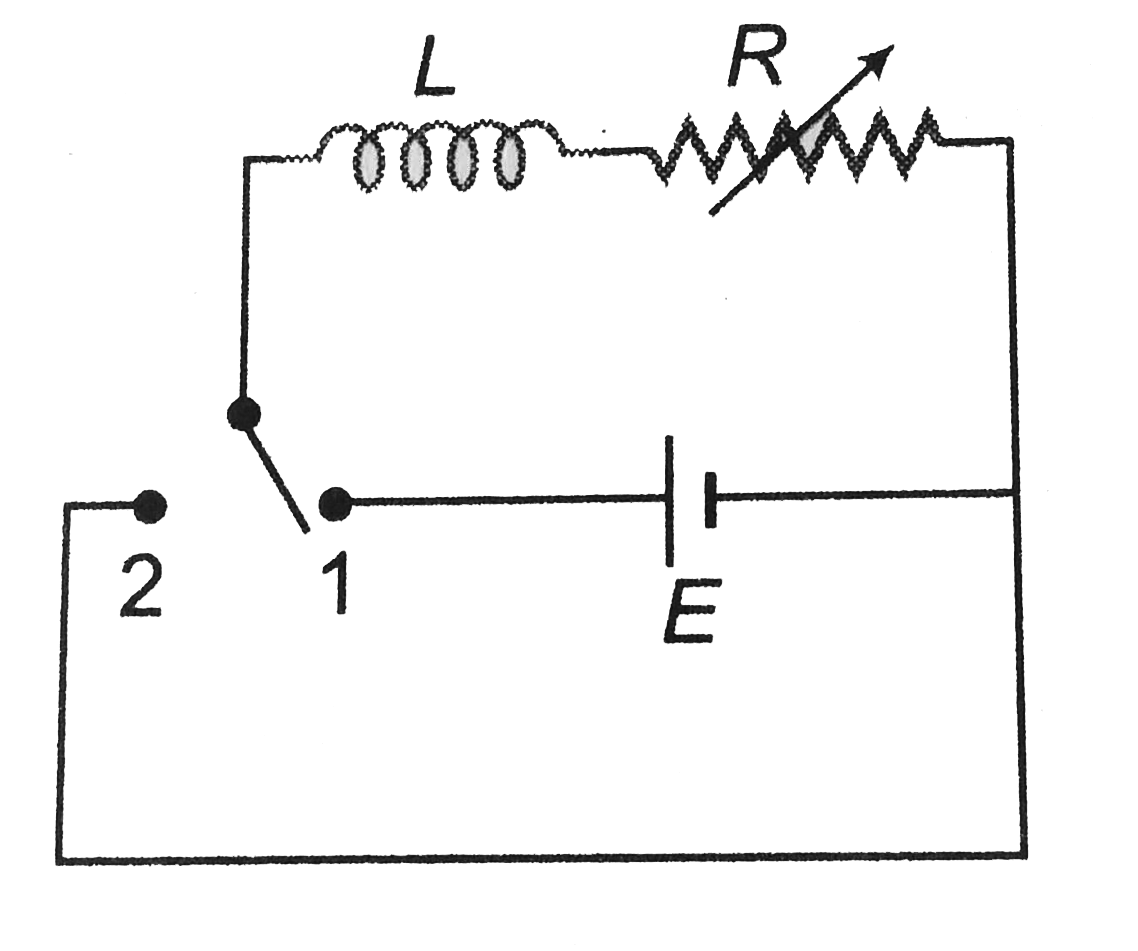
View SolutionIn the circuit shown in the figure initialy the switch in position 1 for a long time, then suddenly at t=0 the switch is shifted to position 2. It is required that a constant current should flow in the circuit, the value of resistance R in the circuit
View SolutionIn the circuit shows in Fig. the initail current through the inductor at t=0 is I0. After a time t=L/R, the switch is quickly shifted to position 2.
a. Plot a graph showing the variation of current with time.
b. Calculate the value of current in the inductor at t=32LR.
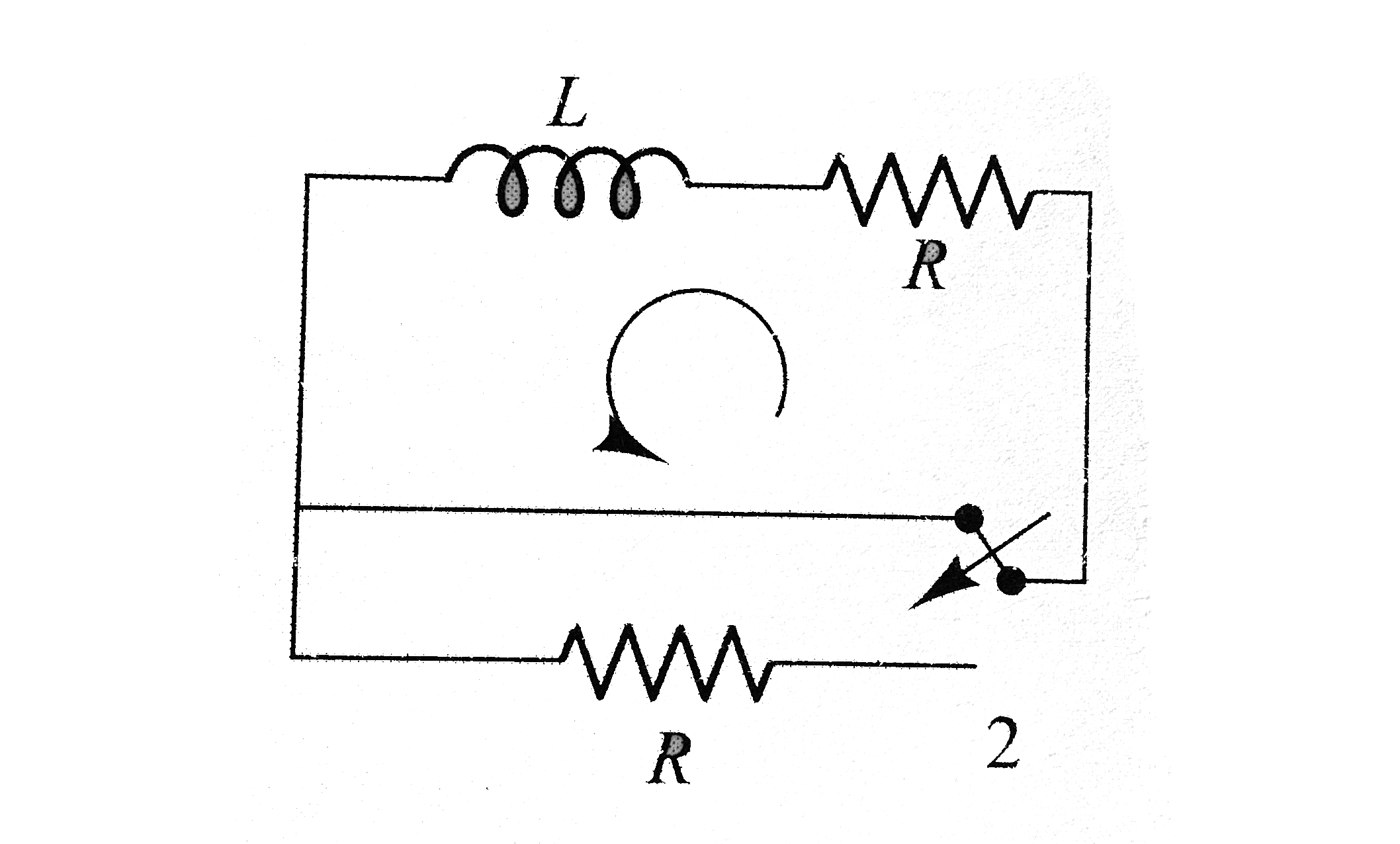
View Solution
