A leaky parallel plate capacitor is filled completely with a material having dielectric constant K=5 and electrical conductivity σ=7.4×10−12Ω−1m−1. If the charge on the capacitor at the instant t=0 is q0=8.55μC, then calculate the leakage current at the instant t=12s.
The correct Answer is:A, C
To solve the problem of finding the leakage current at the instant t=12 seconds for a leaky parallel plate capacitor filled with a dielectric material, we will follow these steps:
Step 1: Identify Given Values
- Dielectric constant, K=5
- Electrical conductivity, σ=7.4×10−12Ω−1m−1
- Initial charge on the capacitor, q0=8.55μC=8.55×10−6C
Step 2: Calculate the Resistivity
The resistivity ρ is given by the reciprocal of the conductivity:
ρ=1σ=17.4×10−12≈1.3514×1011Ω⋅m
Step 3: Calculate the Time Constant τ
The time constant τ for a leaky capacitor can be calculated using the formula:
τ=R⋅C
Where:
- R=ρdA
- C=K⋅ϵ0⋅Ad
Since d and A will cancel out when calculating R⋅C, we can simplify:
τ=ρ⋅K⋅ϵ0
Where ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m.
Substituting the values:
τ=(1.3514×1011)⋅5⋅(8.85×10−12)
Calculating this gives:
τ≈5⋅1.3514⋅8.85≈5⋅1.196≈5.98≈6seconds
Step 4: Calculate the Initial Leakage Current I0
The initial leakage current I0 can be calculated using:
I0=q0τ
Substituting the values:
I0=8.55×10−66≈1.425×10−6A=1.425μA
Step 5: Calculate the Leakage Current at t=12 seconds
The leakage current I(t) at time t can be calculated using the formula:
I(t)=I0⋅e−tτ
Substituting t=12seconds:
I(12)=1.425⋅e−126=1.425⋅e−2
Calculating e−2≈0.1353:
I(12)≈1.425⋅0.1353≈0.193μA
Final Answer
The leakage current at the instant t=12 seconds is approximately 0.193μA.
---
- Dielectric constant, K=5
- Electrical conductivity, σ=7.4×10−12Ω−1m−1
- Initial charge on the capacitor, q0=8.55μC=8.55×10−6C
The resistivity ρ is given by the reciprocal of the conductivity:
ρ=1σ=17.4×10−12≈1.3514×1011Ω⋅m
The time constant τ for a leaky capacitor can be calculated using the formula:
τ=R⋅C
Where:
- R=ρdA
- C=K⋅ϵ0⋅Ad
τ=ρ⋅K⋅ϵ0
Where ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m.
τ=(1.3514×1011)⋅5⋅(8.85×10−12)
Calculating this gives:
τ≈5⋅1.3514⋅8.85≈5⋅1.196≈5.98≈6seconds
The initial leakage current I0 can be calculated using:
I0=q0τ
Substituting the values:
I0=8.55×10−66≈1.425×10−6A=1.425μA
The leakage current I(t) at time t can be calculated using the formula:
I(t)=I0⋅e−tτ
Substituting t=12seconds:
I(12)=1.425⋅e−126=1.425⋅e−2
Calculating e−2≈0.1353:
I(12)≈1.425⋅0.1353≈0.193μA
The leakage current at the instant t=12 seconds is approximately 0.193μA.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
An isolated parallel plate capacitor has circular plates of radius 4.0cm. If the gap is filled with a partially conducting material of dielectric constant K and conductivity 5.0×10−14Ω−1m−1. When the capacitor is charged to a surface charge density of 15μC/cm2, the initial current between the plates is 1.0μA?
a. Determine the value of dielectric constant K.
b. If the total joule heating produced is 7500J, determine the separation of the capacitor plates.
View SolutionThe space between the plates of a parallel plate capacitor is completely filled with a material of resistivity 2×1011Ωm and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the plates is 20μF. Find the leakage current if a potential difference 2500V is applied across the capacitor.
View SolutionThe space between the plates orf a parallel plate capacitor is completely filled with a meterail of resistaivity 2×1011Ωm and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the paltes is 20uF. Find the leakage current if a potential difference 2500 V is applied across the capacitor.
View SolutionA parallel plate capacitor is made of two circular plates separated by a distance 5mm and with a dielectric of dielectric constant 2.2 between them. When the electric field in the dielectric is 3×104V/m the charge density of the positive plate will be close to:
View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA large parallel plate capacitor, whose plates have an area of 1m2 and are separated from each other by 1 mm, is being charged at a rate of 25Vs−1 . If the dielectric constant 10, then the displacement current at this instant is
View SolutionA parallel plate capacitor is to be designed with a voltage rating 1 KV using a material of dielectric constant 3 and dielectric strength about 107Vm−1. [Dielectric strength is the maximum electric field a material can tolerate without break down, i.e, without starting to conduct electrically through partial ionization. For safety, we should like the field never to exceed say 10% of the dielectric strength]. What minimum area of the plates is required to have a capacitance of 50 pF ?
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1, k2 and k3 as shown. If a isngle dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
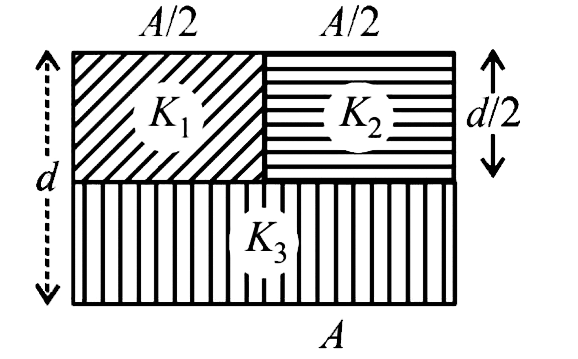
View Solution

