Find equivalent capacitance between points A and B. [Assume each conducting plate is having same dimensions and neglect the thickness of the plate ε0Ad=7μF where A is area of plate]<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_VOL_4_C25_E01_045_Q01.pngwh=80%mx-autosty≤=background:white;>
7μF
11μF
12μF
15μF
The correct Answer is:B
C=ε0Ad=7μF
The equivalent circuit is as shown in figure.
CAB=117C=117(7μF)
=11μF
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
Find out equivalent capacitance between A and B. (take each plate Area = A)
View SolutionFind the equivalent capacitance between point a and b in the following arrangement of the plates .
View SolutionFind the equivalent capacitance between A and B.A: area of each plate, d: separation between the plates.
View SolutionFind out equivalent capacitance between A and B. (take each plate Area = A and distance between two conjugative plates is d)
View SolutionThe equivalent capacitance between P and Q in the figure is (area of each plate is A and separation between two consecutive plates is d)
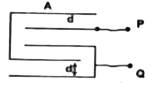
View SolutionThe equivalent capacitance of the arrangement shown in figure, if A is the area of each plate is
View SolutionDerive an expression for the capacitance of a parallel plate capacitor in terms of the areas of the plates and the distance between them. Assume there is a vacuum in between the plates with the electric field between the plates E=σε0 (where the symbols have their usual meaning).
View SolutionFind the capacitance between A and B if three dielectric slabs of dielectric constants K1areaA _(2)andthick≠ssd_(2))are∈sertedbetweentheplatesofaparal≤llate∩aci→rofplateareaA.(Giventˆthedistancebetweenthetwoplatesisd_(1)=d_(2)+d_(2).)
.View SolutionFind out the capacitance of parallel plate capacitor of plate area A and plate separation d.
View SolutionForce between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
View Solution