A block of mass is relesed from rest from a height onto a smooth surface of mass fitted with an ideal spring of stiffness . find the maximum compression in the spring.

Method 1: a. As no external force in horizontal direction, the linear momentum will be conserved in horizonta direction. Let the velocity of block and wedge be a and respectively up to the case when the block reaches on horizontal surface on the wedge.
...............i
Mechanical energy is also conserved in this case
and
Method 2 : Applying work energy theorem from centre of mass frame
also,
b. Initial linear mometum to of the system is zero and there is no external force on the system., hence at the time of maximum compression of spring the linear momentum of the system should be zero. Hence final kinetic energy should be zero.
Hence,
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Exercise 1.1
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Exercise 1.2
Explore 23 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A smooth block of mass m is released from rest from a height h. It slides and compresses the spring of stiffness k. Find the maximum compression of the spring .
Taking block spring a system. Now external force is doing work on system and no non-conservative force is present. The mechanincal energy should be conserved.
ΔK+ΔU=0
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
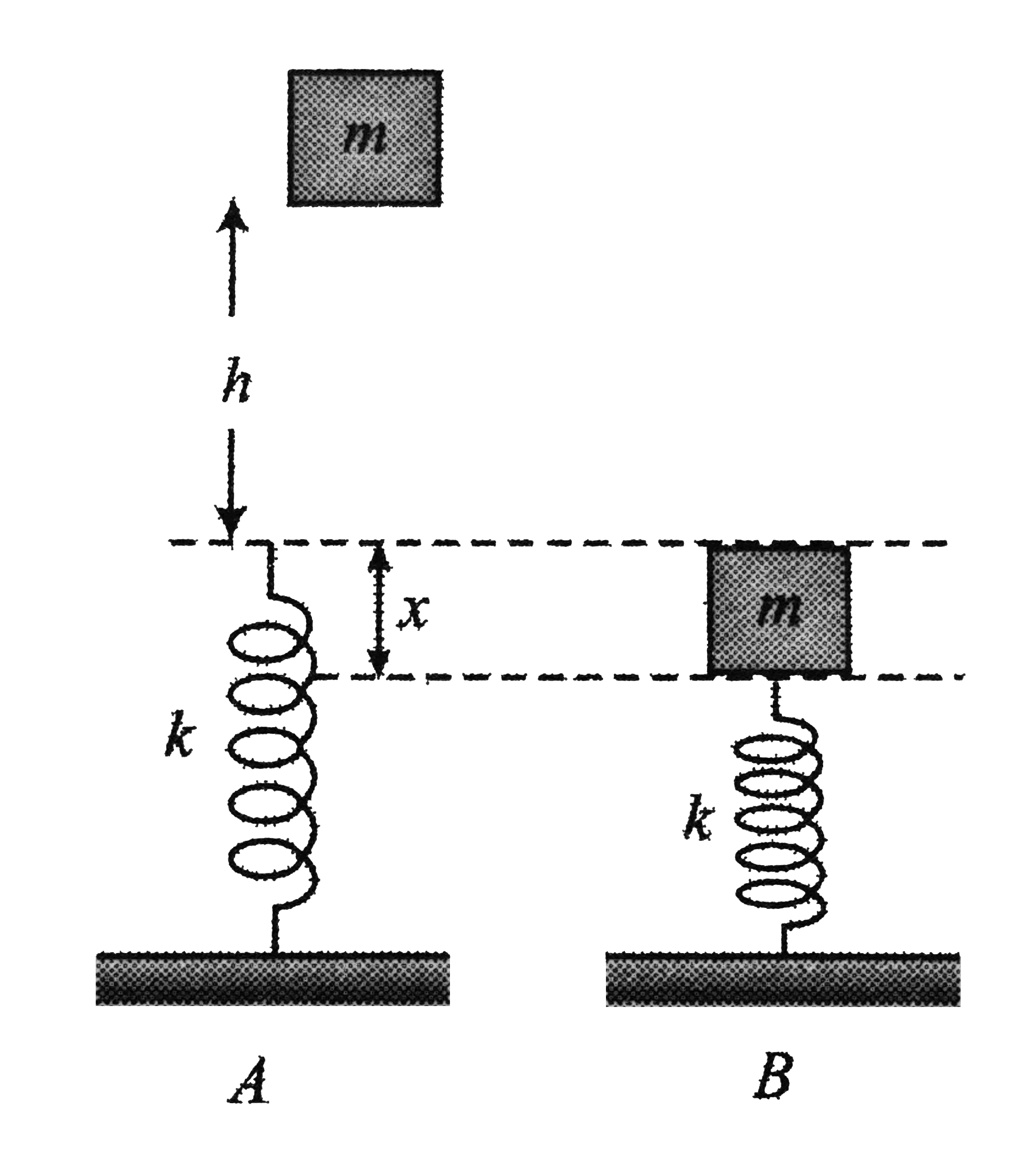
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.

a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100N/m and block comes to rest after compressing spring by 1 m, find the distance travelled by the block before it comes t o rest.

View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest

View Solution

